Attention is what I first need
Last updated on:7 days ago
An attention function can map a query and a set of key-value pairs to an output. Attention is widely used in deep learning models’ architecture. It can mimic cognitive attention by enhancing the essential parts of the input data and fading out the rest.
Attention
Background
The attention we utilize here is self-attention. Self-attention, also called intra-attention, is an attention mechanism relating to different positions of a single sequence. Compared to attention, especially additive attention in RNNs, self-attention has scaled dot product, mask, softmax, and mat-multiplication operations (more complex).
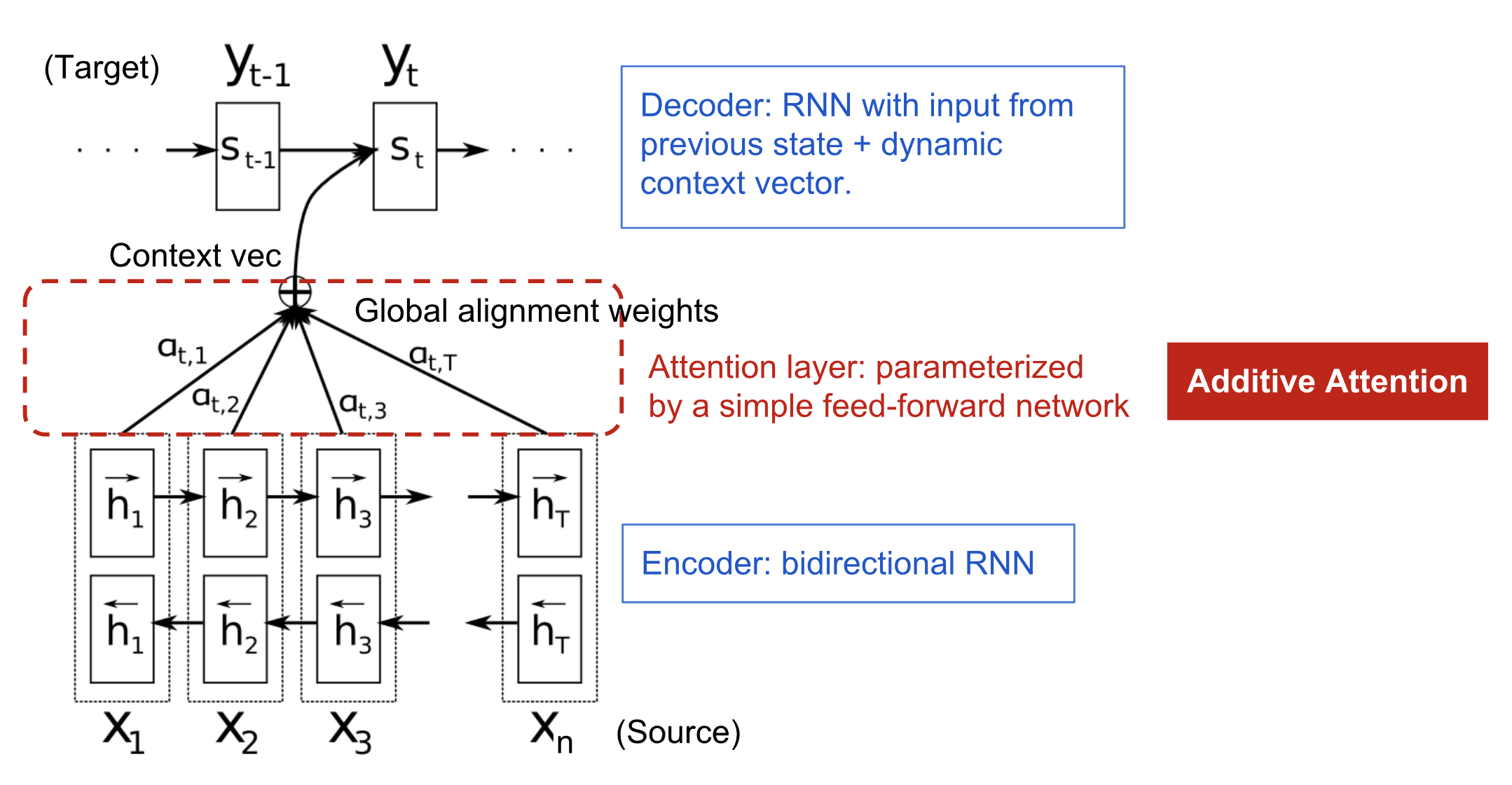
Attention model
$\alpha ^{< t, t’ >}$ means how much should you be paying attention to the $t’$ French words when you’re trying to generate the $t$, English word.
Scaled dot-product attention
The key/value/query concepts come from retrieval systems. For example, when you type a query to search for some video on Youtube, the search engine will map your query against a set of keys (video title, description, etc.) associated with candidate videos in the database, then present you the best matched videos (values).
Queries: the vector representing a word
Keys- Values: the vectors of memory
Q = interesting questions about the words in a sentence
K = qualities of words given a Q
V = specific representations of words provided a Q
In a comment, Q, K, V answer how much the keys match your query to get the desired values.
Queries and keys have the dimension of $d_k$, and values have the dimension of $d_v$. Queries and keys are operated by dot-product, division by $\sqrt{d_k}$, and softmax to attain weight on the values.
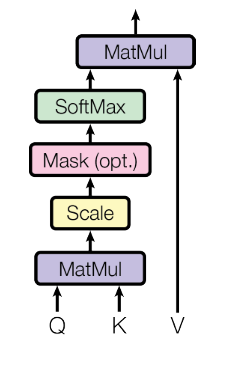
$$\text{Attention} (Q, K, V) = \text{softmax} (\frac{QK^T}{\sqrt{d_k}}) V$$
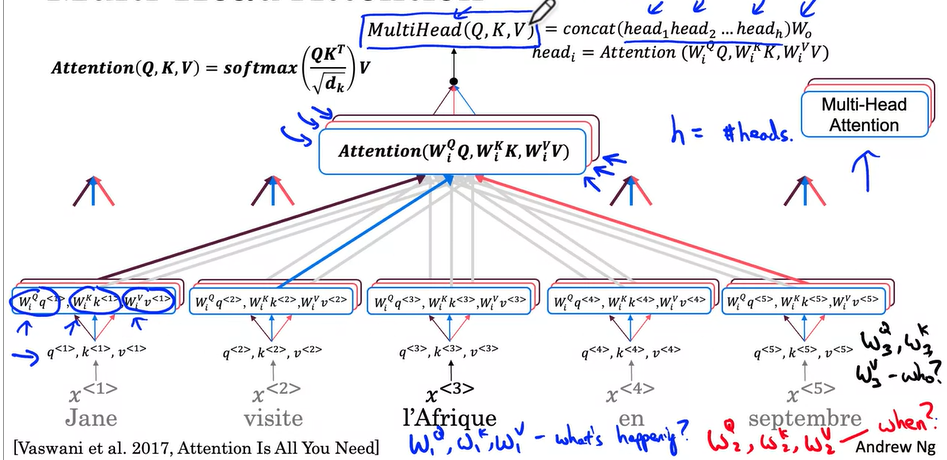
Multi-Head attention
Head: each time you calculate the self-attention sequence is called a head.
$$\text{MultiHead} (Q, K, V) = \text{Concat} (\text{head}_1, …, \text{head}_h) W^O$$
where $$\text{head}_i = \text{Attention} (QW_i^Q, KW_i^K, VW_i^V )$$
The projections are parameter matrices $W^Q_i \in R^{d_{\text{model}} \times d_k}$, $W^K_i \in R^{d_{\text{model}} \times d_k}$, $W^V_i \in R^{d_{\text{model}} \times d_v}$, $W^O \in R^{hd_v \times d_{\text{model}}}$. eg. $h = 8$, $d_k = d_v = d_{\text{model}}/h = 64$
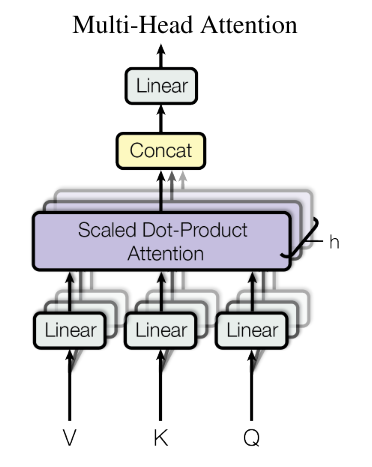
The $h$ times of scaled dot-product attention with efficient operation process. Compute all of the heads in parallel, dependent on each other.
$i$ here represents the computed attention weight matrix associated with the $i$ th “head” in a sentence.
Mask out
Mask out between scale and softmax operations is used to prevent leftward information flow in the decoder to preserve the auto-regressive property (Data leakage). This masking, combined with the fact that the output embeddings are offset by one position, ensures that the predictions for position $i$ can depend only on the known outputs at positions less than $i$.
def generate_square_subsequent_mask(sz):
mask = (torch.triu(torch.ones((sz, sz), device=DEVICE)) == 1).transpose(0, 1)
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
return mask
def create_mask(src, tgt):
src_seq_len = src.shape[0]
tgt_seq_len = tgt.shape[0]
tgt_mask = generate_square_subsequent_mask(tgt_seq_len)
src_mask = torch.zeros((src_seq_len, src_seq_len),device=DEVICE).type(torch.bool)
src_padding_mask = (src == PAD_IDX).transpose(0, 1)
tgt_padding_mask = (tgt == PAD_IDX).transpose(0, 1)
return src_mask, tgt_mask, src_padding_mask, tgt_padding_masksrc_padding_mask and tgt_padding_mask switch the dimension of themselves. e.g. src.shape = torch.Size([27, 128]), src_padding_mask .shape = torch.Size([128, 27]).
tgt_input = tgt[:-1, :]
src_mask, tgt_mask, src_padding_mask, tgt_padding_mask = create_mask(src, tgt_input)
logits = model(src, tgt_input, src_mask, tgt_mask, src_padding_mask, tgt_padding_mask, src_padding_mask)
optimizer.zero_grad()
tgt_out = tgt[1:, :]
loss = loss_fn(logits.reshape(-1, logits.shape[-1]), tgt_out.reshape(-1))There are offsets for tgt. tgt_input is from the beginning to the last-second position. tgt_out is from the second position to the last position.
tgt[:, 0]
tensor([ 2, 20, 26, 16, 1170, 809, 18, 58, 85, 337, 1340, 6,
3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
tgt[:-1, 0]
tensor([ 2, 20, 26, 16, 1170, 809, 18, 58, 85, 337, 1340, 6,
3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
tgt[1:, 0]
tensor([ 20, 26, 16, 1170, 809, 18, 58, 85, 337, 1340, 6, 3,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])Masking out is setting to $- \infty$ all values in the input of the softmax which correspond to illegal connections. softmax it would be $0$.
Code:
attn_mask = attn_mask.masked_fill(key_padding_mask, float("-inf"))if attn_mask is not None:
attn += attn_mask
attn = softmax(attn, dim=-1)Position-wise feed-forward networks
We apply feed-forward network to process output from one attention layer in a way to better fit the input for the next attention layer.
$$\text{FFN}(x) = \max (0, xW_1 + b_1) W_2 + b_2$$
Code:
self.linear1 = Linear(d_model, dim_feedforward, **factory_kwargs)
self.dropout = Dropout(dropout)
self.linear2 = Linear(dim_feedforward, d_model, **factory_kwargs)
self.dropout2 = Dropout(dropout)
# feed forward block
def _ff_block(self, x: Tensor) -> Tensor:
x = self.linear2(self.dropout(F.relu(self.linear1(x))))
return self.dropout2(x)Attention weight
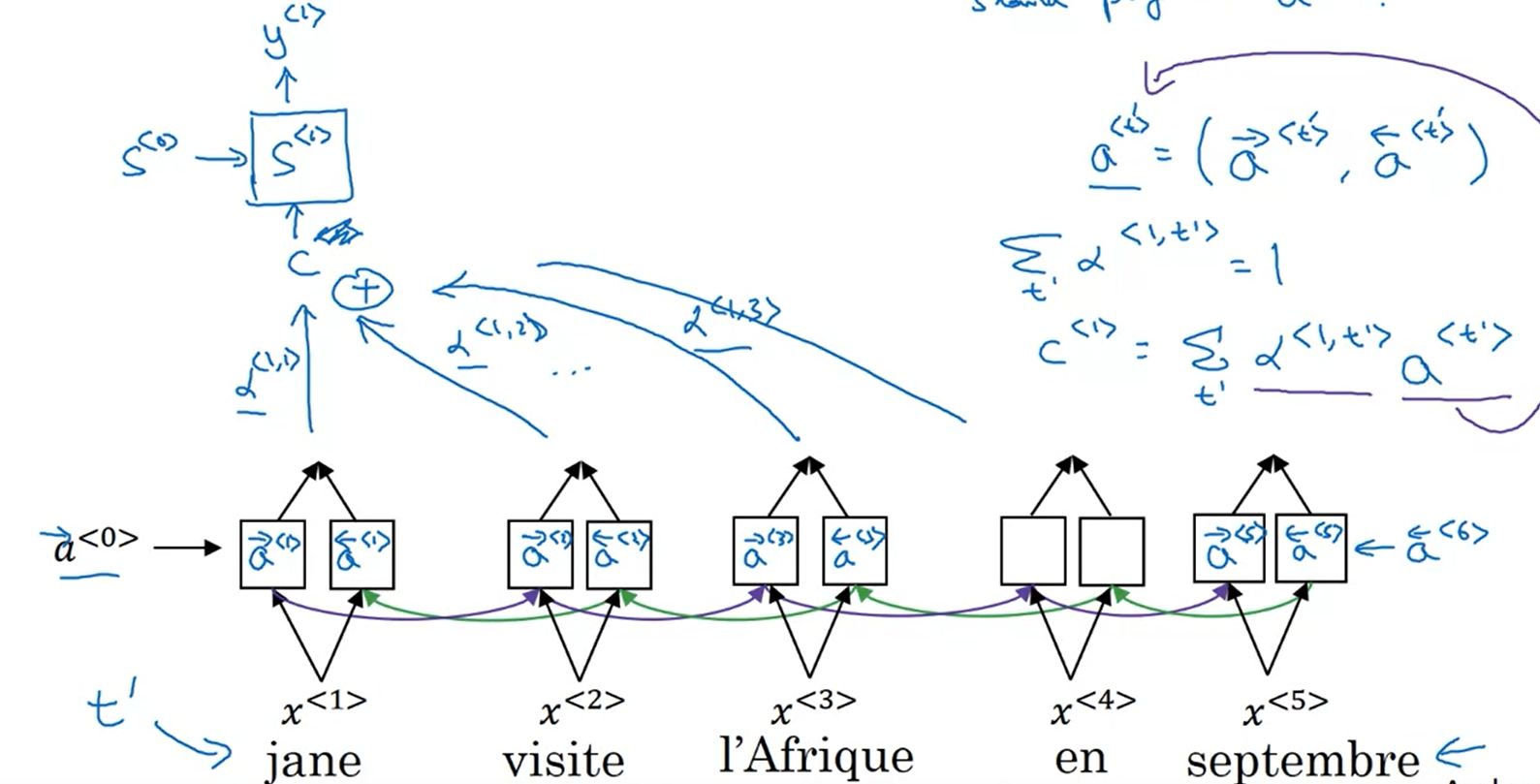
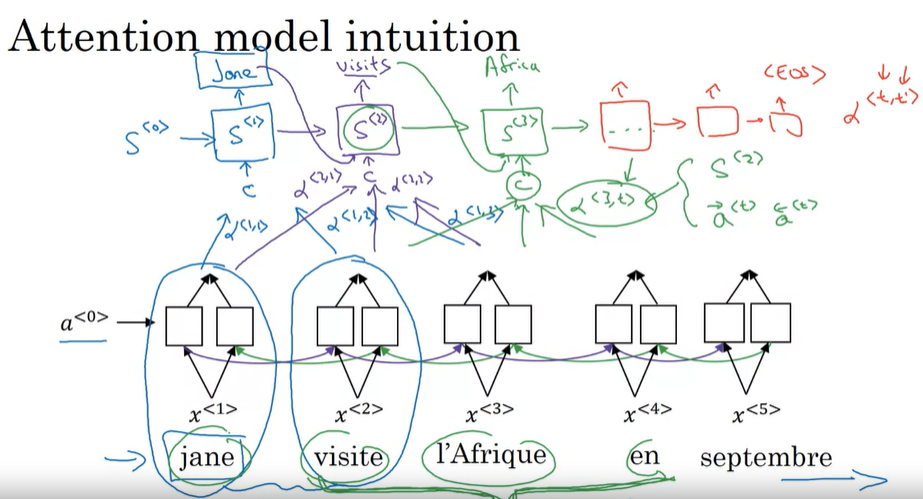
Attention weight: $\alpha^{<t, t’>}$ means the amount of attention that $y^{< t >}$ should pay to $a^{< t’ >}$.
$$\alpha^{<t, t’>} = \frac{exp(e^{<t, t’>})}{\sum^{T_x} {t’ = 1} exp(e^{<t, t’>})}$$
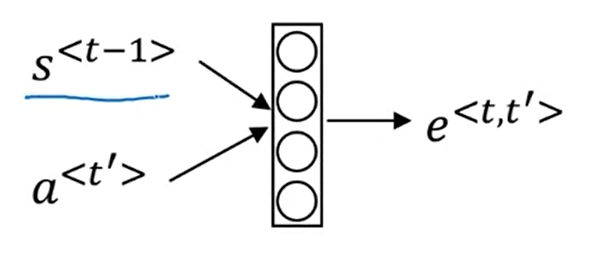
The network learns where to “pay attention” by learning the values $e^{<t,t’>}$, which are computed using a small neural network:
We can’t replace $s^{< t-1 >}$ with $s^{< t >}$ as an input to this neural network. This is because $s^{< t >}$ depends on $\alpha^{<t, t’>}$ which in turn depends on $e^{<t, t’>}$; so at the time we need to evaluate this network, we haven’t computed $s^{< t >}$ yet.
We expect $\alpha^{<t, t’>}$ to be generally larger for values of $a^{< t’ >}$ that are highly relevant to the value the network should output for $y^{< t >}$. (Note the indices in the superscripts.)
$$\sum_{t^{‘}} \alpha^{<t,t^{‘}>} = 1$$
(Note the summation is over $t^{‘}$.)
Why self-attention?
- The total complexity per layer is low.
- The amount of computation can be parallelized.
- The path length between long-range dependencies is short.
A self-attention layer connects all positions with a constant number of sequentially executed operations. Generally, sequence length $n$ is smaller than the representation dimensionality $d$.

Efficient attention methods
Sparse attention, low-rank adaptation, and kernel linearisation.
Sparse attention limits the number of tojens each query could attend to. The sparse pattern could be either pre-defined or learnable.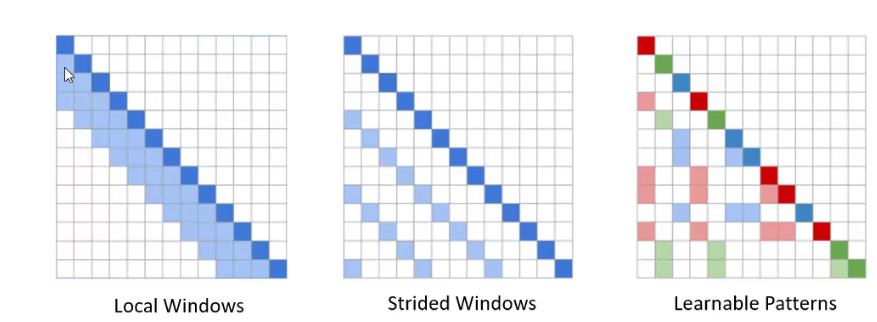
Most low-rank approximation can be viewed as compressing the key-vbalue memory.
The compression step could be conducted via:
- Linear/convolutional projections.
- Downsampling.
- Another lightweight attention module.
Q&A
9. Why is positional encoding important in the translation process? (Check all that apply)
- [x] Position and word order are essential in sentence construction of any language.
- [ ] It helps to locate every word within a sentence.
It is used in CNN and works well there.
-[x] Providing extra information to our model.
10.Which of these is a good criteria for a good positional encoding algorithm?
-[x] It should output a unique encoding for each time-step (word’s position in a sentence).
-[x] Distance between any two time-steps should be consistent for all sentence lengths.
-[x] The algorithm should be able to generalize to longer sentences.
None of the these.
Reference
[1] Deeplearning.ai, Sequence Models
[2] Wiki, Attention (machine learning)
[3] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Ł. and Polosukhin, I., 2017. Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).
[4] What exactly are keys, queries, and values in attention mechanisms?
[5] What is the role of feed forward layer in Transformer Neural Network architecture?
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
