Last updated on：9 months ago

A knowledge graph (KG) is a method to integrate data using graph connected model. Recently, researchers have shown interest in combining KG with deep learning.

Introduction

In knowledge representation and reasoning, a knowledge graph(KG) is a knowledge base that uses a graph-structured data model or topology to integrate data. Knowledge graphs are often used to store interlinked descriptions of entities - objects, events, situations or abstract concepts - while also encoding the semantics underlying the used terminology.

A knowledge graph is a multi-relational graph composed of entities (nodes) and relations (different types of edges). Each edge is represented as a triple of the form (head entity, relation, tail entity), also called a fact, indicating that two entities are connected by specific relation.

It is widely used in graphical neural network (GNN).

Background

The web has considerable scale information, but automatically extracting the knowledge at scale is challenging. Moreover, transforming the candidate facts into helpful knowledge is difficult.

Knowledge graph identification: The task of removing noise, inferring missing information, and determining which candidate facts should be included in a knowledge graph.

Example

Example 1:

For the sentence, “Fido the dog stole a bone from Mary’s backyard”.

We can use (h, r, t) (head entity, relation, tail entity) to represent them.

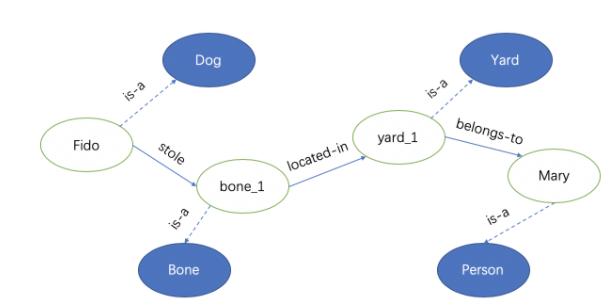
{(Fido, is-a, Dog), (Fido, stole, bone_1), (bone_1, is-a, Bone), (bone_1, located-in, yard_1), (yard_1, is-a, Yard), (yard_1, belongs-to, Mary), (Mary, is-a, Person)}

Example 2:

Rectangles and eclipse: entities

Dotted lines: uncertain information

Solid lines: ontological constraints

Double lines: co-referent entities found with entity resolution

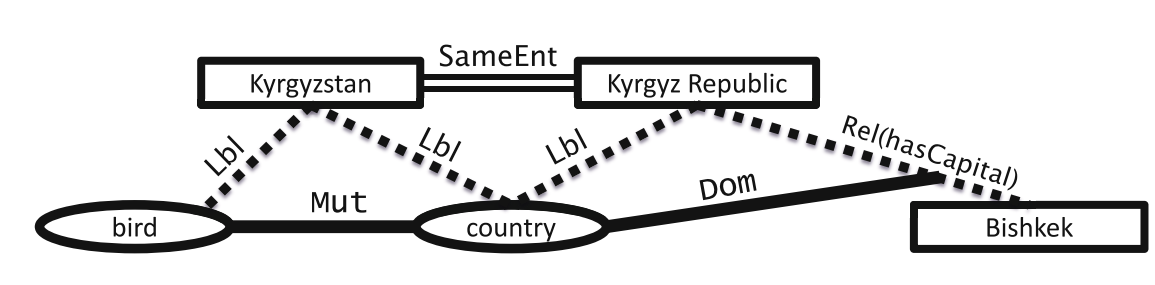
Characteristics

The Knowledge Graph also helps us understand the relationships between things. It can also help you make some unexpected discoveries.

Google KG: The Knowledge Graph enables you to search for things, people or places that Google knows about—landmarks, celebrities, cities, sports teams, buildings, geographical features, movies, celestial objects, works of art and more—and instantly get information that’s relevant to your query.

It is effective in structured data, but the underlying symbolic nature of such triples usually makes KGs hard to manipulate.

Example dataset

FB15k-237

entities.dict

0 /m/0vm5t
1 /m/07fb6
2 /m/06nm1

relations.dict

0 /organization/organization/headquarters./location/mailing_address/state_province_region
1 /education/educational_institution/colors
2 /people/person/profession

train.txt

/m/027rn /location/country/form_of_government /m/06cx9
/m/017dcd /tv/tv_program/regular_cast./tv/regular_tv_appearance/actor /m/06v8s0
/m/07s9rl0 /media_common/netflix_genre/titles /m/0170z3

wn18rr

entities.dict

0 00260881
1 00260622
2 01332730

relations.dict

0 _hypernym
1 _derivationally_related_form
2 _instance_hypernym

train.txt

00260881 _hypernym 00260622

01332730 _derivationally_related_form 03122748

06066555 _derivationally_related_form 00645415

Application in deep learning

Convolutional 2D knowledge graph embeddings

For link prediction.

el: entities, rel: relation

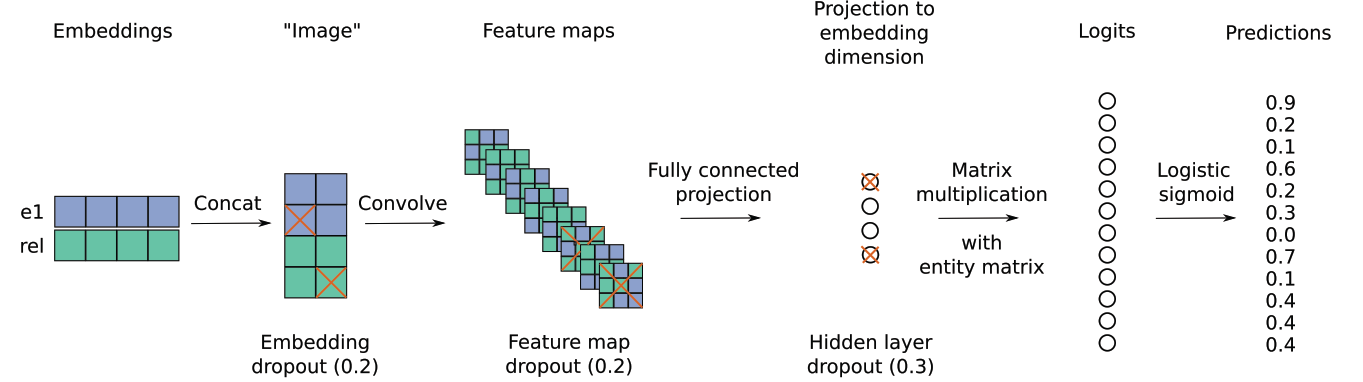
Code:

import torch
from torch.nn import functional as F, Parameter
from torch.nn.init import xavier_normal_, xavier_uniform_

class ConvE(torch.nn.Module):
    def __init__(self, args, num_entities, num_relations):
        super(ConvE, self).__init__()
        self.emb_e = torch.nn.Embedding(num_entities, args.embedding_dim, padding_idx=0) # A simple lookup table that stores embeddings of a fixed dictionary and size.
        self.emb_rel = torch.nn.Embedding(num_relations, args.embedding_dim, padding_idx=0)
        self.inp_drop = torch.nn.Dropout(args.input_drop)
        self.hidden_drop = torch.nn.Dropout(args.hidden_drop)
        self.feature_map_drop = torch.nn.Dropout2d(args.feat_drop)
        self.loss = torch.nn.BCELoss()
        self.emb_dim1 = args.embedding_shape1
        self.emb_dim2 = args.embedding_dim // self.emb_dim1

        self.conv1 = torch.nn.Conv2d(1, 32, (3, 3), 1, 0, bias=args.use_bias)
        self.bn0 = torch.nn.BatchNorm2d(1)
        self.bn1 = torch.nn.BatchNorm2d(32)
        self.bn2 = torch.nn.BatchNorm1d(args.embedding_dim)
        self.register_parameter('b', Parameter(torch.zeros(num_entities)))
        self.fc = torch.nn.Linear(args.hidden_size,args.embedding_dim)
        print(num_entities, num_relations)

    def init(self):
        xavier_normal_(self.emb_e.weight.data)
        xavier_normal_(self.emb_rel.weight.data)

    def forward(self, e1, rel):
        e1_embedded= self.emb_e(e1).view(-1, 1, self.emb_dim1, self.emb_dim2)
        rel_embedded = self.emb_rel(rel).view(-1, 1, self.emb_dim1, self.emb_dim2)

        stacked_inputs = torch.cat([e1_embedded, rel_embedded], 2)

        stacked_inputs = self.bn0(stacked_inputs)
        x= self.inp_drop(stacked_inputs)
        x= self.conv1(x)
        x= self.bn1(x)
        x= F.relu(x)
        x = self.feature_map_drop(x)
        x = x.view(x.shape[0], -1)
        x = self.fc(x)
        x = self.hidden_drop(x)
        x = self.bn2(x)
        x = F.relu(x)
        x = torch.mm(x, self.emb_e.weight.transpose(1,0))
        x += self.b.expand_as(x)
        pred = torch.sigmoid(x)

        return pred

PyTorch allows a tensor to be a View of an existing tensor. View tensor shares the same underlying data with its base tensor.

t = torch.rand(4, 4)
t.view(-1, 1) # reshape tensor t into (16, 1)
t.view(1, -1) # reshape tensor t into (1, 16)

To explain:

e1_embedded= self.emb_e(e1).view(-1, 1, self.emb_dim1, self.emb_dim2)

I give an example.:

emb_e = torch.nn.Embedding(2, 3, padding_idx=0)
emb_e(torch.tensor(0)).view(-1, 1)
# return tensor([[0.],
#         [0.],
#         [0.]], grad_fn=<ViewBackward>)

So the e1_embedded get the e1 entity in (embedding_dim, 1) shape.

Knowledge graph embedding (KGE) models

KGE learn a low-rank vector representation of knowledge entities and relations that can be used to rank knowledge assertions according to their factuality.

KGE model initializes all embedding vectors using random noise values. It then uses these embedding to score the set of true and false training facts using a model-dependent scoring function.

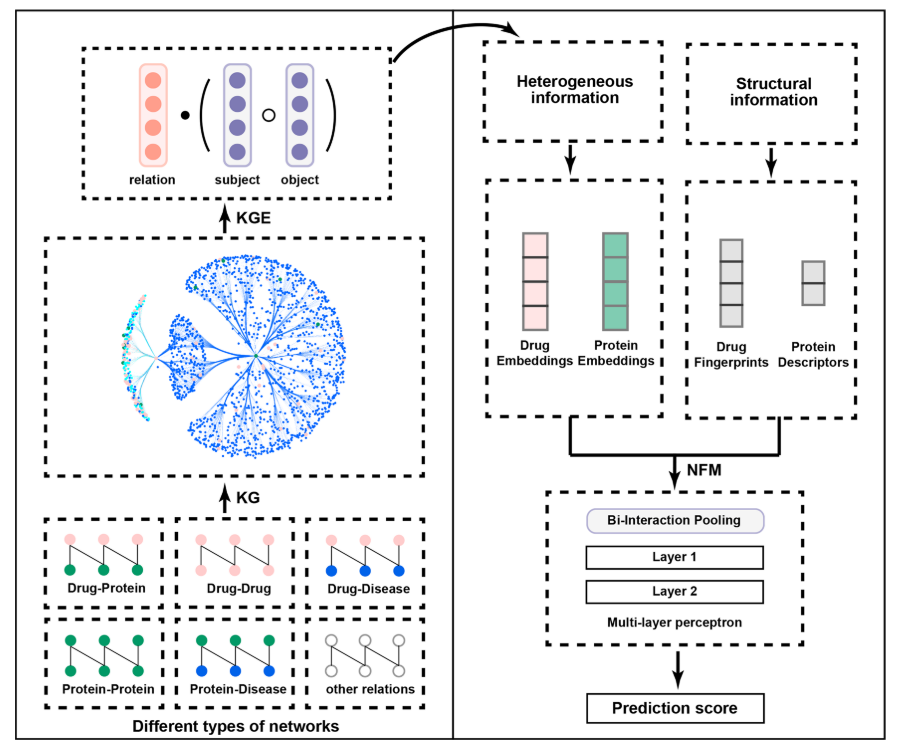
The following figure is a graph schema for a knowledge graph about drugs, their target genes, pathways, diseases and gene networks extracted from KEGG and UniProt databases.

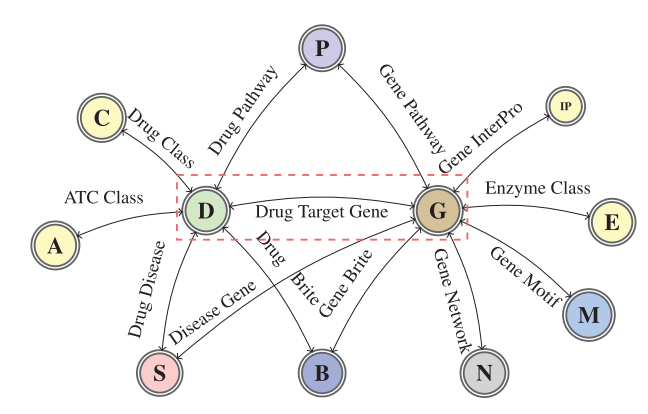
TriModel is a KGE embedding model. Loss function:

$$\mathcal{L}^{\text{TriModel}}_{spo} = -\phi_{spo} + \log ( \sum_{o^{‘}} exp( \phi_{spo^{‘}} ) ) -\phi_{spo} + \text{log} (\sum_{s^{‘}} exp(\phi_{s^{‘}po}))$$

$$+ \frac{\lambda}{3} \sum^K_{k=1} \sum^{3}_{m=1} (\left|e^m_s\right| ^3 + \left|w^m_p\right| ^3 + \left|e^m_o\right| ^3)$$

To predict drug target proteins:

Casual relations

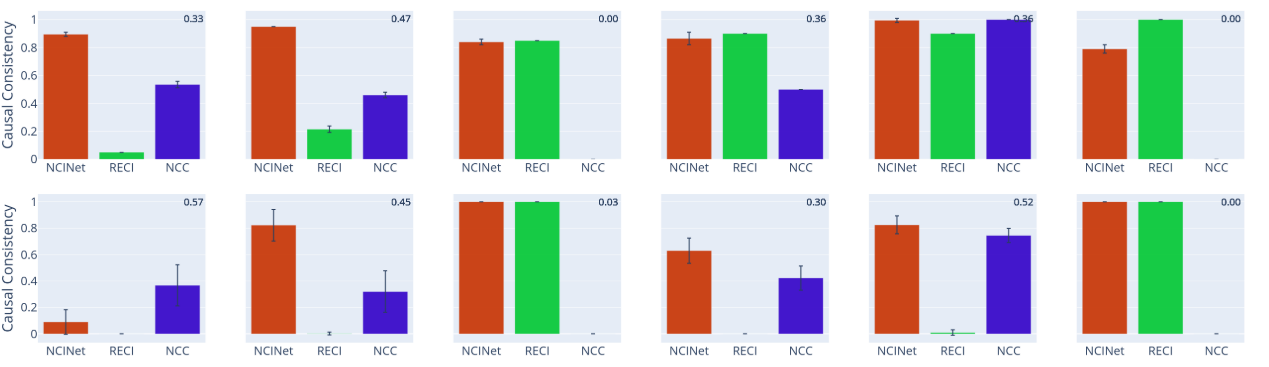
There are several possible causal relations between pairs of random variables.

In most cases, across both 3D shapes and CASIA-WebFace, the causal relationship between the learned representations is highly consistent with that of the labels. It can be mimicked by representation learning algorithms.

Codes:

p_config = np.random.randint(0, 5)  # 6 different causal cases
p_fun=self.idx
print(p_fun)      
funs=['linear','hadamard','bilinear','cubicspline','nn']
fun=funs[p_fun]
if p_config ==0: # X->Y
    X=self.initial_data(npairs,ndimsx)
    causal_mechanism=self.mechanism[fun](ndimsx,ndimsx)
    X=causal_mechanism(X)
    causal_mechanism=self.mechanism[fun](ndimsx,ndimsy)
    Y=causal_mechanism(X)
    label = 1
elif p_config ==1: # Y->X
    Y=self.initial_data(npairs,ndimsy)
    causal_mechanism=self.mechanism[fun](ndimsy,ndimsy)
    Y=causal_mechanism(Y)
    causal_mechanism=self.mechanism[fun](ndimsy,ndimsx)
    X=causal_mechanism(Y)
    label = 2
elif p_config ==2: #X Y
    X=self.initial_data(npairs,ndimsx)
    Y=self.initial_data(npairs,ndimsy)
    causal_mechanism=self.mechanism[fun](ndimsx,ndimsx)
    X=causal_mechanism(X)
    causal_mechanism=self.mechanism[fun](ndimsy,ndimsy)
    Y=causal_mechanism(Y)
    label=0
elif p_config ==3: #X<-Z->Y
    ndimsz=min(ndimsx,ndimsy)
    Z=self.initial_data(npairs,ndimsz)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsz)
    Z=causal_mechanism(Z)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsx)
    X=causal_mechanism(Z)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsy)
    Y=causal_mechanism(Z)
    label = 0
elif p_config ==4: #X<-Z->Y and X->Y
    ndimsz=min(ndimsx,ndimsy)
    Z=self.initial_data(npairs,ndimsz)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsz)
    Z=causal_mechanism(Z)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsx)
    X=causal_mechanism(Z)
    causal_mechanism=self.mechanism[fun](ndimsx,ndimsy,ndimsz)
    Y=causal_mechanism(X,Z)
    label = 1
elif p_config == 5:  # X<-Z->Y and Y->X
    ndimsz=min(ndimsx,ndimsy)
    Z=self.initial_data(npairs,ndimsz)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsz)
    Z=causal_mechanism(Z)
    causal_mechanism=self.mechanism[fun](ndimsz,ndimsy)
    Y=causal_mechanism(Z)
    causal_mechanism=self.mechanism[fun](ndimsy,ndimsx,ndimsz)
    X=causal_mechanism(Y,Z)
    label = 2

Reference

[1] Knowledge graph

[2] Pujara, J., Miao, H., Getoor, L. and Cohen, W., 2013, October. Knowledge graph identification. In International Semantic Web Conference (pp. 542-557). Springer, Berlin, Heidelberg.

[3] Introducing the Knowledge Graph: things, not strings

[4] Wang, Q., Mao, Z., Wang, B. and Guo, L., 2017. Knowledge graph embedding: A survey of approaches and applications. IEEE Transactions on Knowledge and Data Engineering, 29(12), pp.2724-2743.

[5] 什么是知识图谱（Knowledge Graph）（上）

[6] Dettmers, T., Minervini, P., Stenetorp, P. and Riedel, S., 2018, April. Convolutional 2d knowledge graph embeddings. In Thirty-second AAAI conference on artificial intelligence.

[7] Mohamed, S.K., Nováček, V. and Nounu, A., 2020. Discovering protein drug targets using knowledge graph embeddings. Bioinformatics, 36(2), pp.603-610.

[8] Wang, L. and Boddeti, V.N., 2022. Do learned representations respect causal relationships?. arXiv preprint arXiv:2204.00762.

[9] human-analysis/causal-relations-between-representations

Deep learning Machine learning

knowledge graph

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

Some small bugs and features of Deep learning Previous

Multithreading PyQt applications with QThreadPool Next

What is knowledge graph and what its relation to deep learning?