We use word embedding to feature representation. The contents of the blog are a note rearranging of course Sequence Model.

Introduction

Learn high dimensional feature vectors that give a better across different words

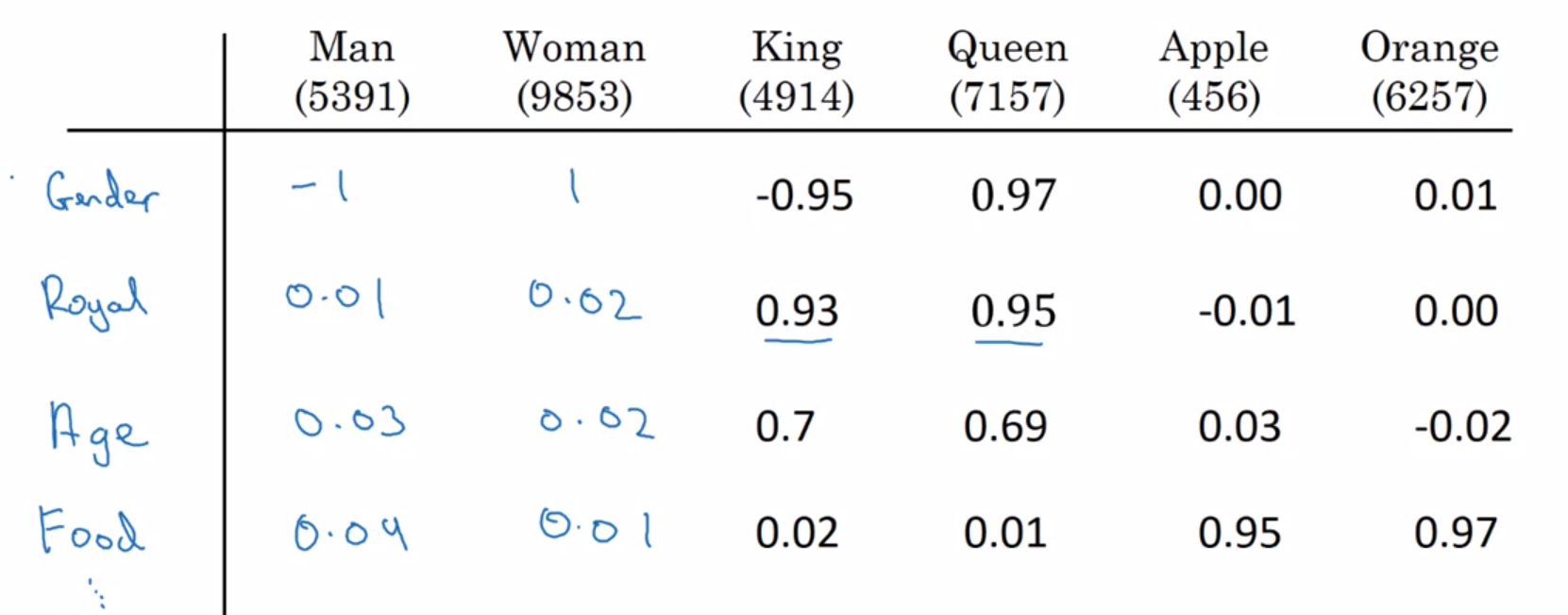
Suppose you learn a word embedding for a vocabulary of 10000 words. The dimension of word vectors is usually smaller than the vocabulary size. The most common sizes for word vectors range between 50 and 1000.

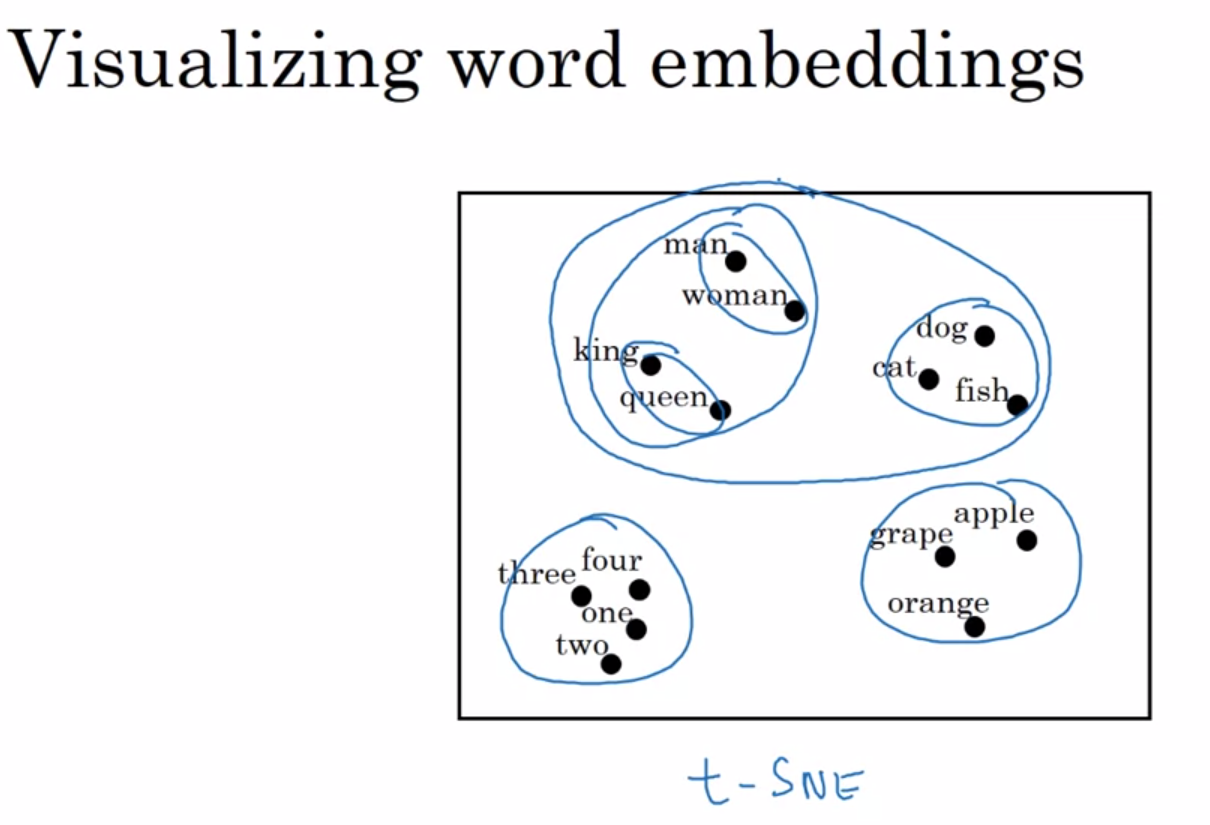
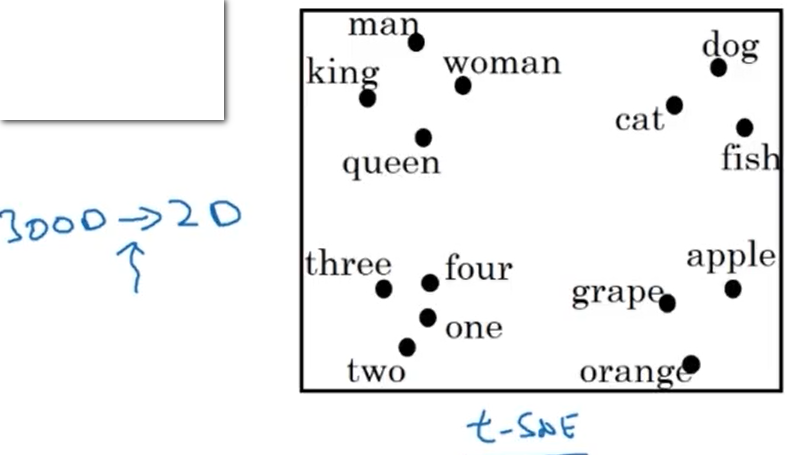
t-SNE visualisation

t-SNE can be used to map similar feature vectors. It is a non-linear dimensionality reduction technique.

Distance

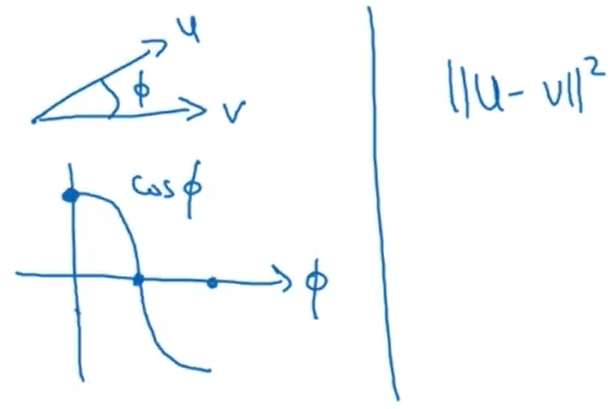
Cosine similarity is a good way to compare the similarity between pairs of word vectors. Note that L2 (Euclidean) distance also works. Using a pre-trained set of word vectors for NLP applications is often a great way to get started.

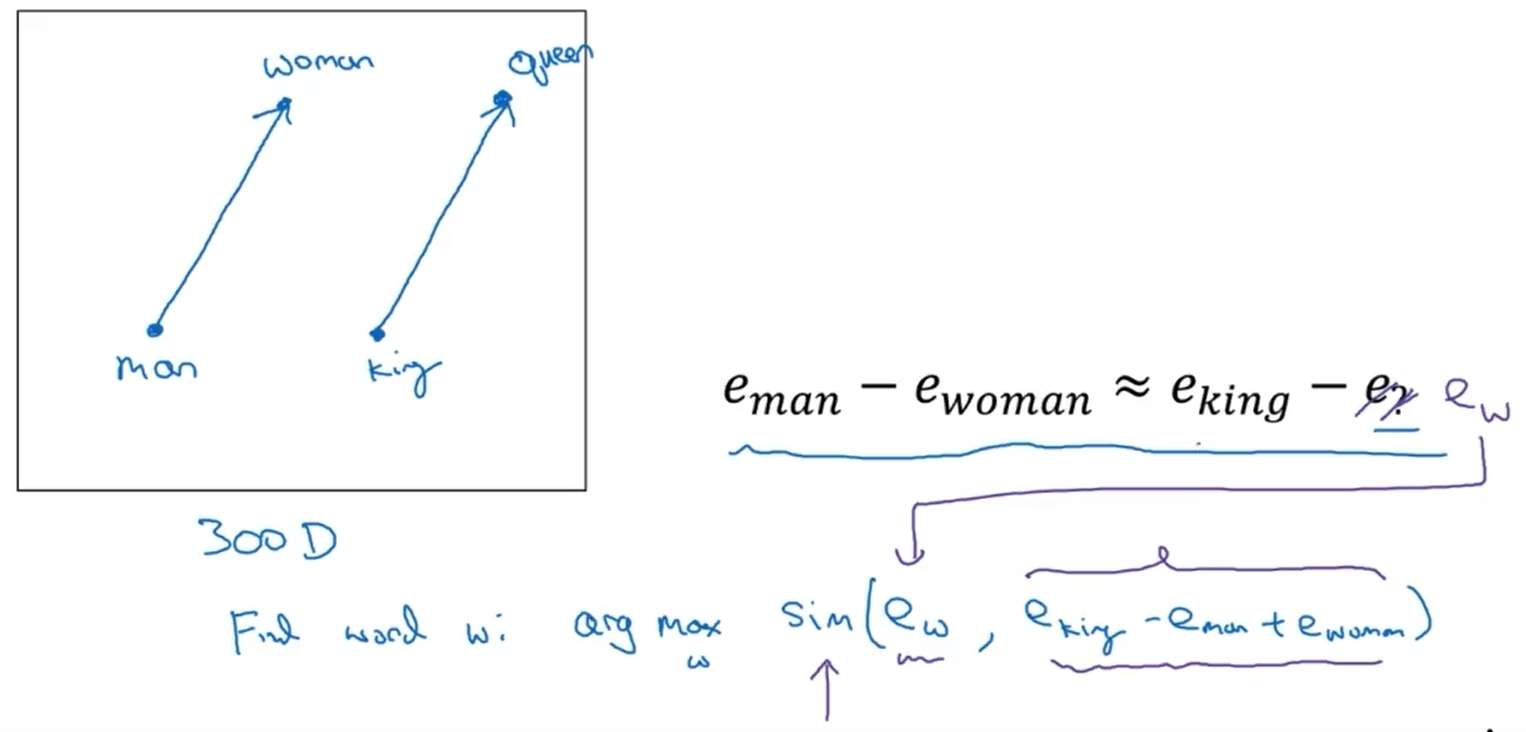
Cosine similarity

$sim(u,v) = \frac{u ^ T _ v}{||u||_2 ||v||_2}$

Question:

Which of these equations do you think should hold for a good word embedding? (Check all that apply)

$e _ {man} - e_{woman} \approx e _{queen} - e _{king}$

$e _ {man} - e_{king} \approx e _ {queen} - e _ {woman}$

-[x] $e _ {man} - e_ {king} \approx e _{woman} - e _{queen}$

-[x] $e _ {man} - e_ {woman} \approx e _ {king} - e_ {queen}$

Embedding matrix

We pick a given word and try to predict its surrounding words or vice versa.

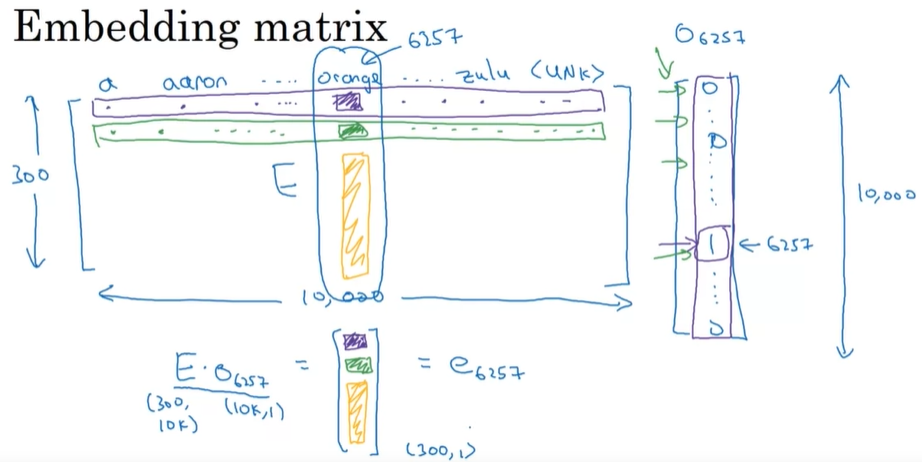
From 300 x 10000 to 300 for each (also 300 x 10000).

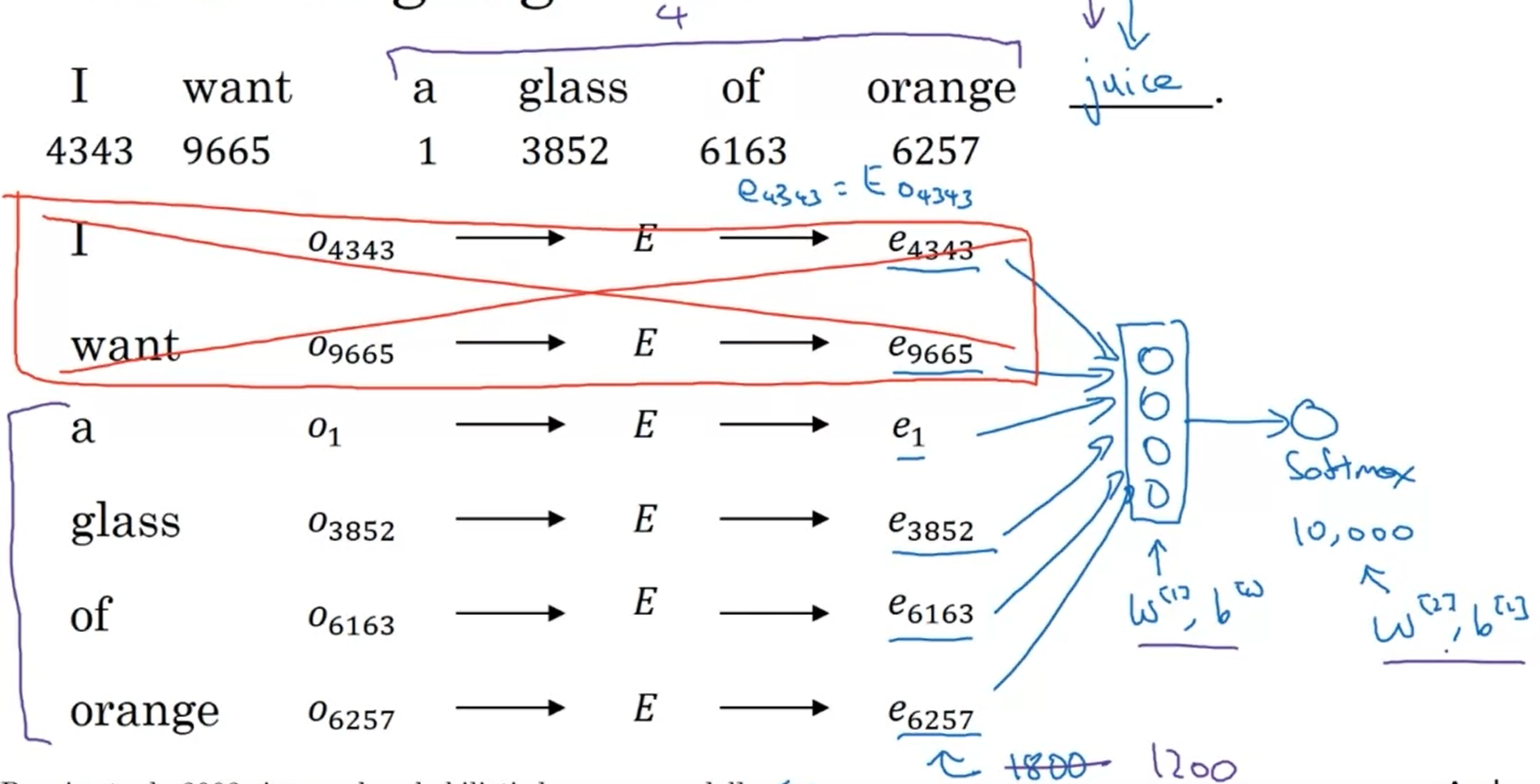
Another context/word pairs

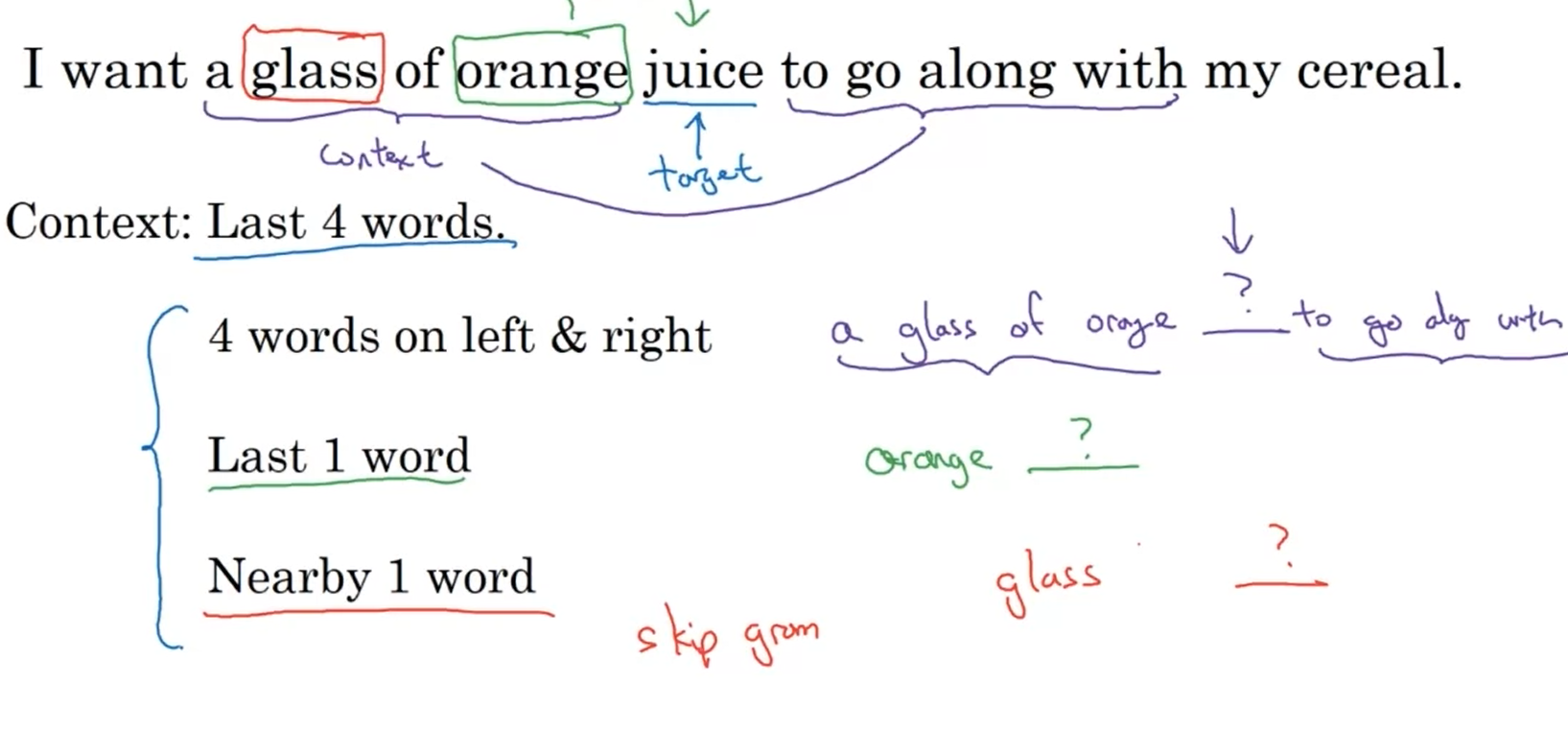
When learning word embeddings, we create an artificial task of estimating $P(\text{target}\mid \text{mid context})$. It is okay if we do poorly on this artificial prediction task; the more important by-product of this task is that we learn a useful set of word embeddings.

$t$ and $c$ are chosen from the training set as nearby words.

Word2Vec

One-hot vectors don’t do an excellent job of capturing the level of similarity between words. Every one-hot vector has the same Euclidean distance as any other one-hot vector.

Vocab size $= 10,000$.

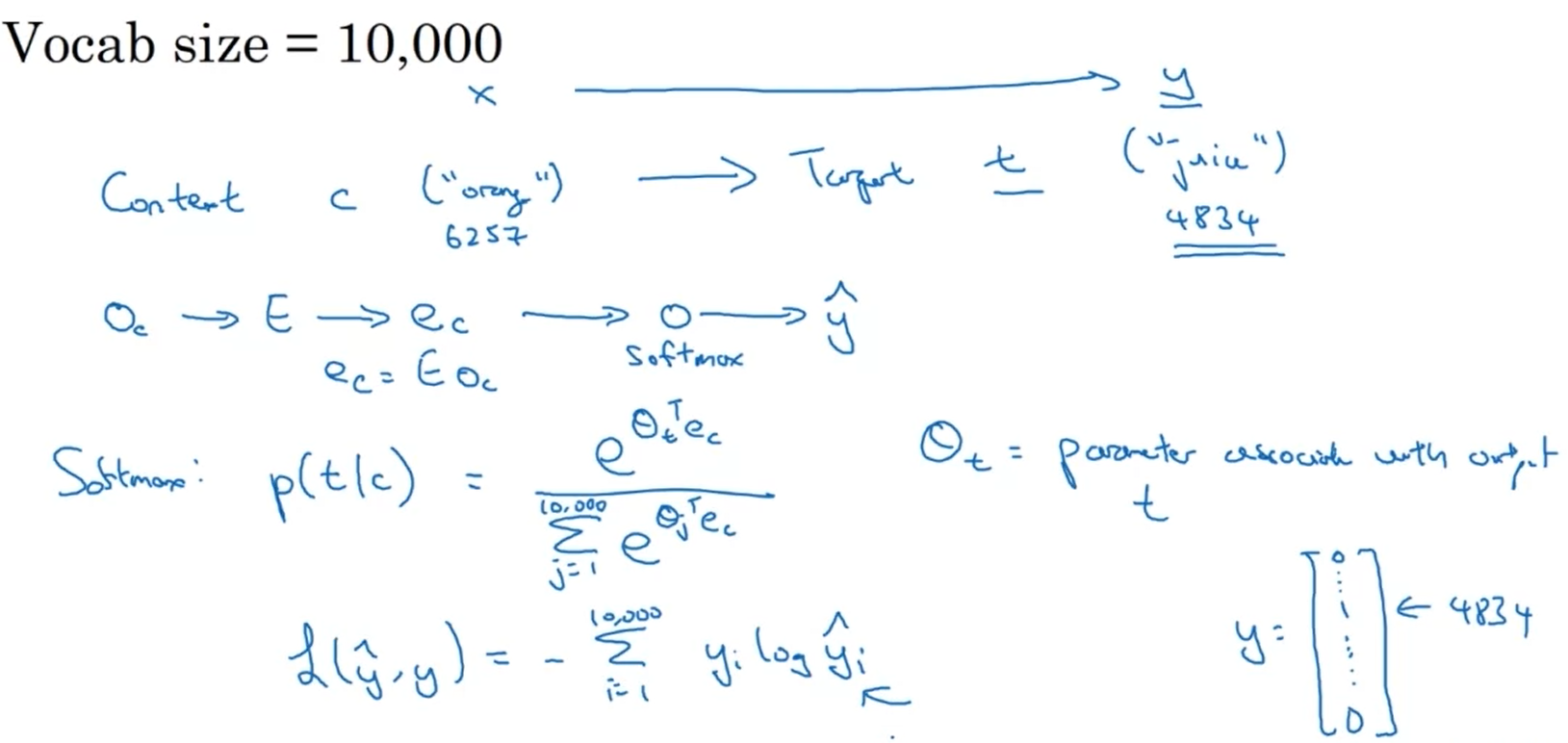
SoftMax classification consumes high computational costs.

Use hierarchical SoftMax.

$$p(t\mid c) = \frac{e^{\theta _ t ^ T e_c}}{\sum ^ {10,000} _ {j=1} e ^ {\theta _ j ^ T e_c}}$$

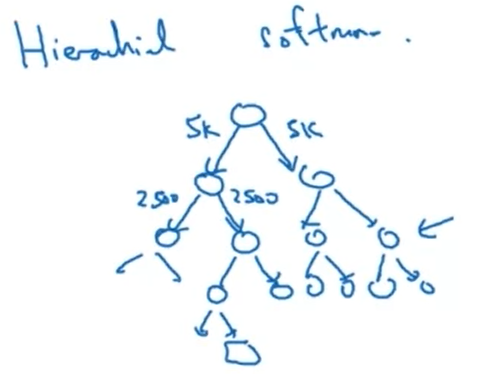
Balance something from the common words together with the less common ones (e.g., the, of, a, and, to).

Question:

Suppose you have a 10000 word vocabulary, and are learning 500-dimensional word embeddings. The word2vec model uses the following softmax function:

$$P(t \mid c) = \frac{e ^ {\theta _ t ^ T e _ c}}{\sum _ {t^{‘} = 1}^{10000} e ^ {\theta _ {t^{‘}} ^ T e _ c}}$$

Which of these statements are correct? Check all that apply.

-[x] $\theta_t$ and $e_c$ are both 500 dimensional vectors.

-[x] $\theta_t$ and $e_c$ are both trained with an optimization algorithm such as Adam or gradient descent.

$\theta_t$ and $e_c$ are both 10000 dimensional vectors.

After training, we expect $\theta_t$ to be very close to $e_c$ when $t$ and $c$ are the same word.

GloVe word vectors

Embedding vectors, such as GloVe vectors, provide much more helpful information about the meaning of individual words.

Minimize the difference between:

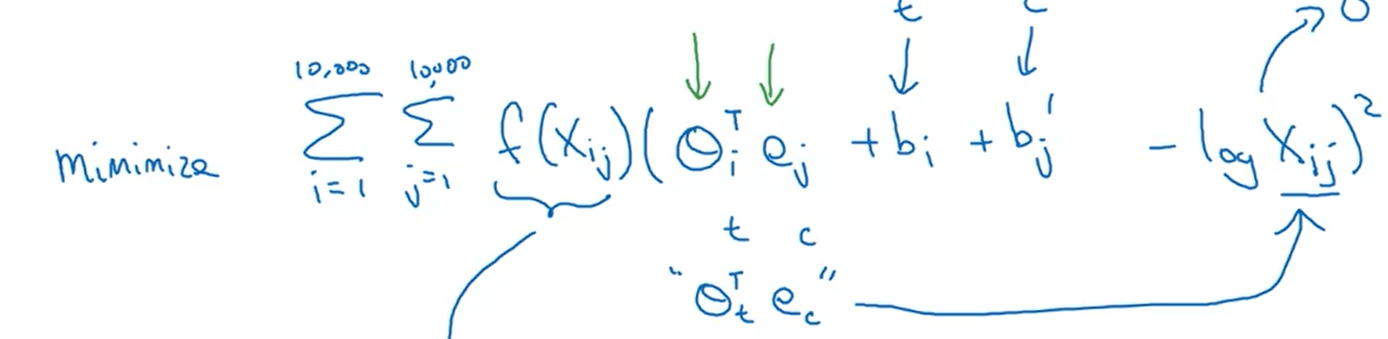
$\theta_i, e_j$ are symmetric. The featurization view of word embeddings.

Question:

Let $A$ be an embedding matrix, and let $o _ {4567}$ be a one-hot vector corresponding to word 4567. Then to get the embedding of word 4567, why don’t we call $A * o _ {4567}$ in Python?

The correct formula is $A^T * o_{4567}$.

-[ ] This doesn’t handle unknown words ().

None of the answers is correct: calling the Python snippet described above is fine.

-[x] It is computationally wasteful.

Suppose the unknown token is added to the vocabulary, and the vocabulary list is passed as an input to the embedding layer. In that case the element-wise operation is valid even for the unknown token.

Suppose you have a 10000 word vocabulary, and are learning 500-dimensional word embeddings. The GloVe model minimizes this objective:

$$\min \sum _ {i=1}^{10,000} \sum _ {j=1}^{10,000} f(X _ {ij}) (\theta _ i ^ T e_j + b_i + b_j^{‘} - \text{log} X_{ij})^2$$

Which of these statements are correct? Check all that apply.

-[x] $X_{ij}$ s the number of times word $j$ appears in the context of word $i$.

-[x] $\theta_i$ and $e_j$ should be initialized to 0 at the beginning of training.

$\theta_i$ and $e_j$ should be initialized randomly at the beginning of training.

-[x] Theoretically, the weighting function $f(.)$ must satisfy $f(0) = 0$.

Debiasing

Word embeddings can reflect gender, ethnicity, age, sexual orientation, and other biases of the text used to train the model.

The problem of bias in word embeddings:

Word embeddings can reflect gender, ethnicity, age, sexual orientation, and other biases of the text used to train the model.

Addressing bias in word embeddings

• Identify bias direction
• Neutralise: for every word that is not definitional, be projected to get rid of bias
• Equalise pairs

Highlight

• If you have an NLP task where the training set is small, using word embeddings can help your algorithm significantly.
• Word embeddings allow your model to work on words in the test set that may not even appear in the training set.
• Training sequence models in Keras (and in most other deep learning frameworks) require a few essential details:
• To use mini-batches, the sequences need to be padded so that all the examples in a mini-batch have the same length.
• An Embedding() layer can be initialised with pretrained values.
• These values can be either fixed or trained further on your dataset.
• If, however, your labelled dataset is small, it’s usually not worth trying to train a sizeable pre-trained set of embeddings.
• LSTM() has a flag called return_sequences to decide if you would like to return every hidden state or only the last one.
• You can use Dropout() right after LSTM() to regularise your network.

Reference

[1] Deeplearning.ai, Sequence model