Dimensionality reduction plays an essential part in speeding up learning processes.

Basic ideas

Data compression

eg. reduce data from 2D to 1D
eg. reduce data from 3D to 2D

Data visualization

1D, 2D, 3D

Principal component analysis/PCA

Try to find a lower dimensional surface, so that the sum value of the square of these group line segment is small.

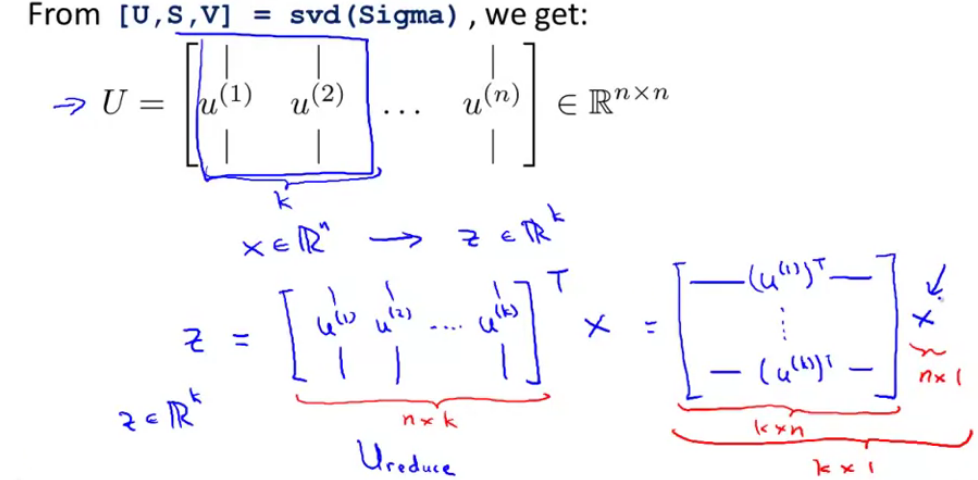
Reduce from n-dimension to k-dimension: find k vector $u^{(1)}, u^{(2)}, …, u^{(K)}$ onto which to project the data to minimize the projection error.

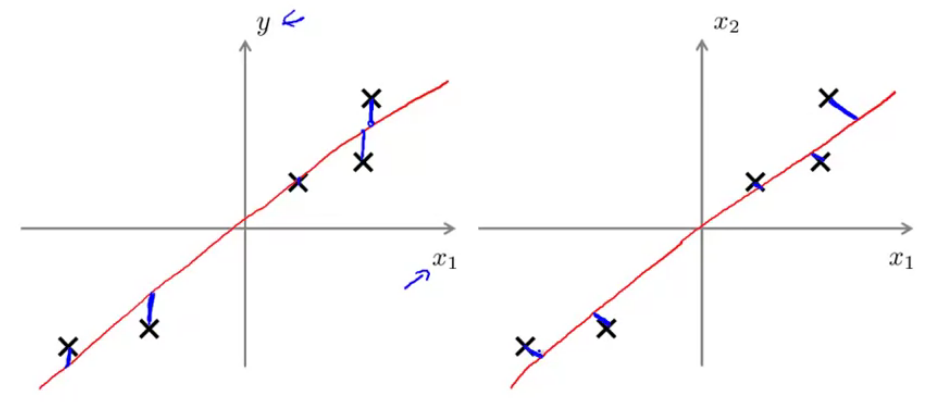
PCA is not linear regression

Linear regression vs. PCA

$X\to y$ VS. treated $x_1, x_2, …, x_m$ equally.

Principal component analysis algorithm

• Pre-processing (feature scaling/mean normalization):

Replace each $x_j^{(i)}$ with $x_j - \mu_j$
Scale features to have comparable range of values.

• Compute covariance matrix: $\sum = \frac{1}{m} \sum_{i=1}^n (x^{(i)}) (x^{(j)}) ^T$

(satisfy symmetric positive definite)

• Compute eigenvectors of matrix $\sum$:

[U, S, V] = svd(Sigma);

Reconstruction from the compressed representation

$$z = U^T_{reduce} x$$
$$X_{approx}^{(1)} = U_{reduce} z^{(1)}$$
$$R^n = (n\times k) (k\times 1) $$

Choosing k the number of principal components

• Average squared projection error: $$\frac{1}{m} \sum^m_{i=1} ||x^{(i)} - x^{(i)}_{approx}|| ^2$$
• Total variation in the data: $\frac{1}{m} \sum^m_{i=1} ||x^{(i)}|| ^2$

Typically, choose k to be smallest value so that
$$\frac{\frac{1}{m} \sum^m_{i=1} ||x^{(i)} - x^{(i)}{approx}|| ^2}{\frac{1}{m} \sum^m{i=1} ||x^{(i)}|| ^2} <= 0.01$$
99% of variance is retained.

Advice for applying PCA

• Extract inputs from an unlabelled dataset
• New training set

Note: mapping $x \to z$ should be defined by running PCA only on the training set. This mapping can be applied as well to the examples $x_cv$ and $x_test$ in the cross validation and test sets

Design of ML system

• Get training set
• Run PCA to reduce $x^{(i)}$ in dimension to get $z^{(i)}$
• Train logistic regression on
• Test on test set: map $$x_{test}^{(i)} \to z^{(i)}_{test}$$

Before implementing PCA, try running whatever you want to do with the original/raw data $x^{(i)}$ first . only if that doesn’t do what you want, then implement PCA and consider using $z^{(i)}$

Reference

[1] Andrew NG, Machine learning