Last updated on：2 years ago

SVM is usually mentioned in Machine Learning. But sometimes I still get confused that how it relates to ML.

Definition

In machine learning, support vector machines/SVMs are supervised learning models with associated learning algorithms that analyse data for classification and regression analysis.

It follows the idea, Input vectors are non-linearly mapped to a very high-dimension feature space

Also, the neural network is a learning model of machine learning. Different learning models with a different cost function, characteristics, application.

Support vector machine is a large margin classifier.

A Support Vector Machine (SVM) performs classification by finding the hyperplane that maximizes the margin between the two classes. The vectors (cases) that define the hyperplane are the support vectors.

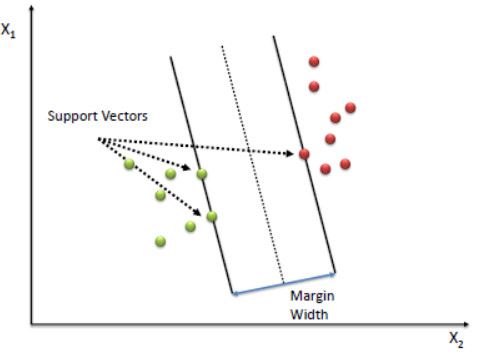
SVM hypothesis

$$\min_\theta C \sum^{m}_{i=1} [y^{(i)} cost_1 (\theta^T x^{(i)}) + (1 - y^{(i)}) cost_0( \theta^T x^{(i)})] + \frac{1}{2} \sum^{n}_{i=1} \theta_j^2$$

Need to specify

Choice of parameter C
Choice of kernel (similarity function)

For C, remember: if C is larger, $\theta$ or $\omega$ is larger, then the model is going to overfit

Kernels

Adapt SVM to develop complex nonlinear classifier

$$f_i = \text{similarity} (x, l^{(i)}) = exp ( - \frac{|| x - l^{(i)}|| ^2}{2 \sigma ^2})$$

Superscript is still the level of layer.

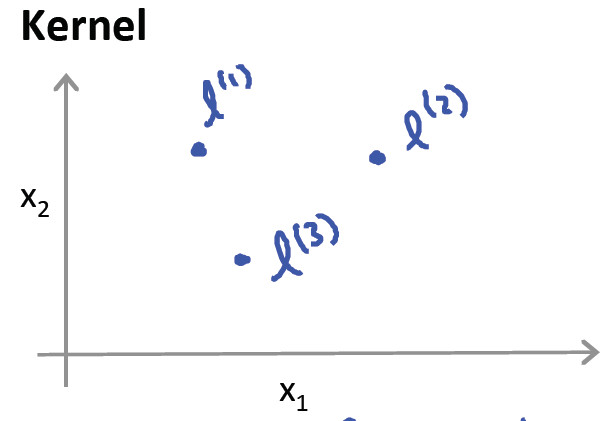
Kernel types

Linear kernel
$$\theta_0 + \theta_1 x_1 + … + \theta_n x_n \ge 0$$

Polynomial kernel

$$ k(x,l) = (x^T l)^2, (x^T l)^3, (x^T l+1)^2, (x^T l + \text{constant})^{\text{degree}}$$
More esoteric

string k, chi-square k, histogram intersection k

Logistic regression vs SVM

If n is larger than m, use logistic regression or SVM without a kernel
With so many features, linear functions can fit very complicated non-linear function
If n is small, m is intermediate
Use SVM with Gaussian kernel
If n is small, m is large
Create/add more features, then use logistic regression or SVM without a kernel

Neural network likely to work well for most of these settings, but maybe slower to train.

SVM in deep learning

Replace softmax by SVM.

Note that prediction using SVMs is exactly the same as using a softmax.

The only difference between softmax and multiclass SVMs is in their objectives parametrized by all of the weight matrices W. Soft- max layer minimizes cross-entropy or maximizes the log-likelihood, while SVMs simply try to find the maximum margin between data points of different classes.