长期以来，计算机视觉和机器人学领域都没有合适和工具来描述三维物体。而四元数正好可以解决这些问题。 方程的公式在实际应用中相当重要，比如在机械臂移动的仿真中，方程组的复杂程度对仿真的速度有着极大的影响。虽然向量是一种简洁的描述运动的系统，但是对于对旋转描述仍然存在不足。

定义

设

$$q = a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k}, a,b,c,d \in R$$

其中，i,j,k满足

$$\mathbf{i}^2 = \mathbf{j}^2 = \mathbf{k}^2 = -1$$ $$\mathbf{i}\mathbf{j} = -\mathbf{j}\mathbf{i} = \mathbf{k}, \mathbf{j}\mathbf{k} = -\mathbf{k}\mathbf{j} = \mathbf{i}, \mathbf{k}\mathbf{i} = -\mathbf{k}\mathbf{i} = \mathbf{j}$$

则称$q$为四元数，而称a为q的实部，记为$Re(q) = a$；称$b\mathbf{i} + c\mathbf{j} + d\mathbf{k}$为q的虚部，记为$Im(q) = b\mathbf{i} + c\mathbf{j} + d\mathbf{k}$。四元数的全体记为Q。

$$Q = {a + b\mathbf{i} + c\mathbf{j} + d\mathbf{k} | a,b,c,d \in R}$$

特别当$c = d = 0$时，q就是复数了，即$q = a + b\mathbf{i} \in C$。在此基础上，若$b = 0$，则q就是实数，即$q = a \in R$。因此，四元数是实数和复数的扩展。

特性

• 四元数相加：

$$(a_{1}+b_{1}\,\mathbf {i} +c_{1}\,\mathbf {j} +d_{1}\,\mathbf {k} )+(a_{2}+b_{2}\,\mathbf {i} +c_{2}\,\mathbf {j} +d_{2}\,\mathbf {k} ) =$$ $$(a_{1}+a_{2})+(b_{1}+b_{2})\,\mathbf {i} +(c_{1}+c_{2})\,\mathbf {j} +(d_{1}+d_{2})\,\mathbf {k}$$

• 乘以一个系数：

$$\lambda (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )=\lambda a+ \lambda b ,\mathbf {i} + \lambda c,\mathbf {j} + \lambda d ,\mathbf {k}$$

• 倒数：

$$(a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )^{-1} = {\frac{1}{a^{2} + b^{2} + c^{2} + d^{2}}}\, (a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} )$$

• 方向向量为单位向量，两两正交。
• 两个四元数的乘积（哈密尔顿乘积 Hamilton product）:

$$q_1 q_2 = ( a 1 + b 1\mathbf{i} + c 1\mathbf{j} + d 1\mathbf{k}) ( a 2 + b 2\mathbf{i} + c 2\mathbf{j} + d 2\mathbf{k})$$

或者

$$q_1 q_2 = -(q_1 \dot q_2) + (q_1 \times q_2)$$

• 绝对值：

$$|q| = \sqrt{q q^{\*}} = \sqrt {q^\* q} = \sqrt{ a^{2} + b^{2} + c^{2} + d^{2} }$$

• 共轭：

$$q^* = a - b\mathbf{i} - c\mathbf{j} - d\mathbf{k}$$

应用

刚体位姿描述

刚体位姿描述有四种方法：姿态矩阵法、姿态角表示法、轴—角表示法和单位四元数法。

姿态角和四元数法在相机坐标系和图像坐标系变换中比较常用。其中，四元数法需要4个非独立参数，表示范围大，不存在奇异点，且旋转运动表示形式简洁，但缺点是不直观。它的定义如下：

$$\mathbf{Q} =\eta + \varepsilon_x \mathbf{i} + \varepsilon_y \mathbf{j} + \varepsilon_z \mathbf{k} = [\eta , \mathbf{\varepsilon}]= [\eta\ \varepsilon_x\ \varepsilon_y\ \varepsilon_z]^T$$

其中，$\eta$为变量部分，$\mathbf{\varepsilon}=[\varepsilon_x\ \varepsilon_y\ \varepsilon_z]^T$为矢量部分。

RGB坐标系

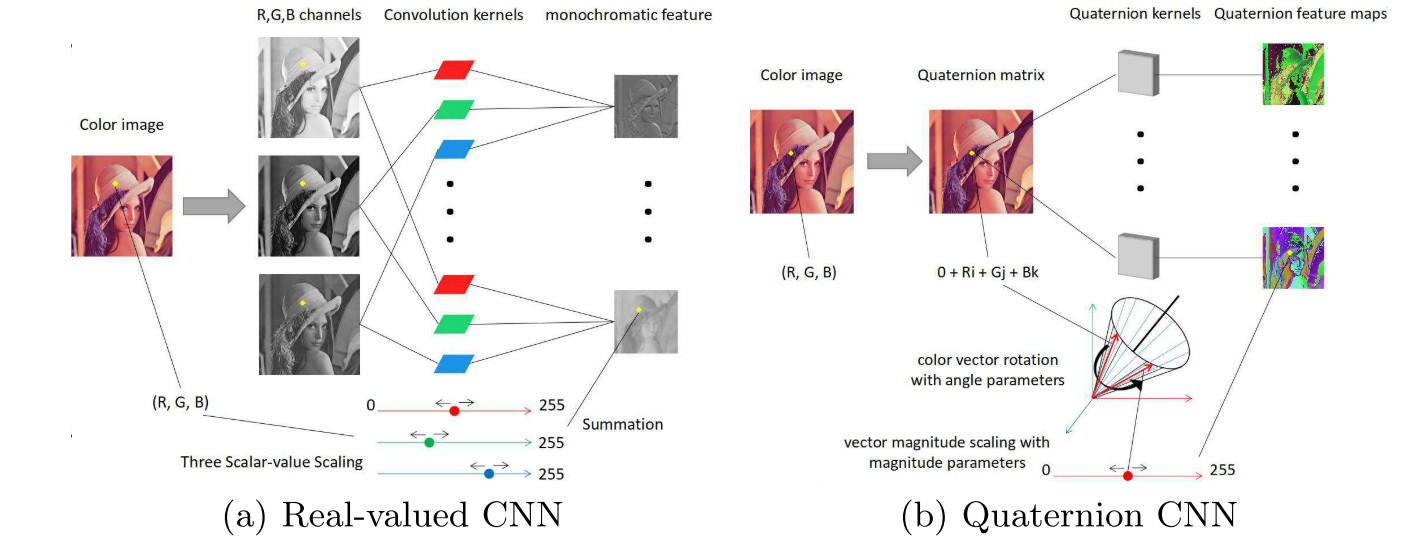
假设旋转向量$\mathbf{q} = [q_1\ q_2\ q_3]^T$绕着轴$\mathbf{\omega} = [\omega_1\ \omega_2\ \omega_3]^T$得到新的向量$\mathbf{p} = [p_1\ p_2\ p_3]^T$（$\mathbf{\omega}$是单位向量）。则

$$\mathbf{p} = \mathbf{\omega}\mathbf{q}\mathbf{\omega} ^*$$

其中，$\mathbf{p}$和$\mathbf{q}$都可以认为是实部为0的四元数，而旋转轴$\mathbf{\omega}$为

$$\mathbf{\omega} = cos\frac{\theta}{2} + sin\frac{\theta}{2}(\omega_1 \mathbf{i} + omega_2 \mathbf{j} + omega_3 \mathbf{k})$$

参考资料

[1] Quaternion

[2] 李文亮，四元数矩阵，国防科技大学出版社

[3] Pervin, E. and Webb, J.A., 1982. Quaternions in computer vision and robotics. CARNEGIE-MELLON UNIV PITTSBURGH PA DEPT OF COMPUTER SCIENCE.

[4] Zhu, X., Xu, Y., Xu, H. and Chen, C., 2018. Quaternion convolutional neural networks. In Proceedings of the European Conference on Computer Vision (ECCV) (pp. 631-647).