FLOPs and MAcs are used for measuring the computer performance.

FLOPs

In computing, floating point operations per second (FLOPS, flops or flop/s) is a measure of computer performance, useful in fields of scientific computations that require floating-point calculations. For such cases it is a more accurate measure than measuring instructions per second.

FLOPs = Floating point operations

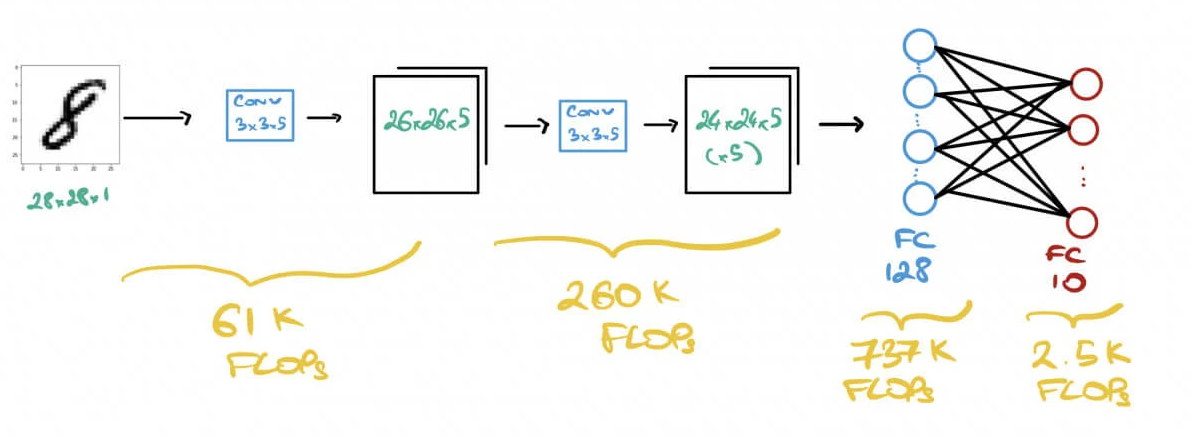
For CNN kernels:

$$\text{FLOPs} = 2HW(C_{\text{in}} K^2 + 1)C_{\text{out}}$$

For FC layers:

$$\text{FLOPs} = (2I - 1)O$$

Most of modern hardware architectures uses FMA instructions for operations with tensors.

FMA computes $a*x + b$ as one operation.

MACs = Multiply–accumulate operations

Roughly, GMACs $\approx$ 0.5 * GFLOPs

Others

FLOPs is abbreviation of floating operations which includes mul / add / div … etc.

MACs stands for multiply–accumulate operation that performs a <- a + (b x c).

As shown in the text, one MACs has one mul and one add. That is why in many places FLOPs is nearly two times as MACs.

However, the application in real world is far more complex. Let’s consider a matrix multiplication example.
A is an matrix of dimension mxn and B is an vector of nx1.

for i in range(m):
    for j in range(n):
        C[i][j] += A[i][j] * B[j] # one mul-add
```     

It would be `mn` `MACs` and `2mn` `FLOPs`. But such implementation is slow and parallelization is necessary to run faster


  ```python
for i in range(m):
    parallelfor j in range(n):
        d[j] = A[i][j] * B[j] # one mul
    C[i][j] = sum(d) # n adds

Then the number of MACs is no longer mn .

When comparing MACs /FLOPs, we want the number to be implementation-agnostic and as general as possible. Therefore in THOP, we only consider the number of multiplications and ignore all other operations.

PS: The FLOPs is approximated by multiplying two.

Reference

MACs, FLOPs, what is the difference?