Face verification requires comparing a new picture against one person’s face, whereas face recognition requires comparing a new picture against K person’s faces. However, both of them are based on the same theory.

What is face recognition

Face recognition is widely used in verification and recognition.

Verification

• Input image name/ID
• Output whether the input image is that of the claimed person

Recognition

• Has a database of K person
• Get an input image
• Output ID if the image is any of the K persons (or “not recognized”)

Differences

• Face verification solves an easier 1:1 matching problem; face recognition addresses a harder 1:K matching problem.
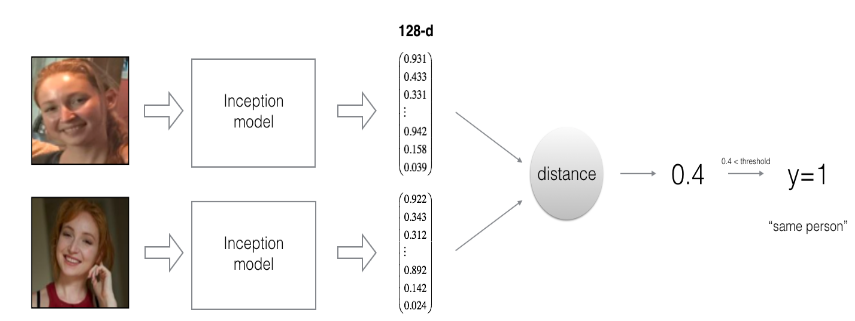
• The same encoding can be used for verification and recognition. Measuring distances between two images’ encodings allows you to determine whether they are pictures of the same person.

One-shot learning

Learn from one example to recognize the person again. eg. 5 person then 6 output (softmax)

Learning a “similarity” function

For verification,

$$d(img1, img2) = \text{degree of difference between images}$$

$$\text{If} d(img1, img2) \begin{bmatrix}
\le \tau \text{“same”} \\
\ge \tau \text{“same”} \\
\end{bmatrix}$$

Q&A

2.Why do we learn a function d(img1, img2)d(img1,img2) for face verification? (Select all that apply.) Given how few images we have per person, we need to apply transfer learning.

-[x] We need to solve a one-shot learning problem.

-[x] This allows us to learn to recognize a new person given just a single image of that person.

-[ ] This allows us to learn to predict a person’s identity using a softmax output unit, where the number of classes equals the number of persons in the database plus 1 (for the final “not in database” class).

The methodology of final choice is used in face recognition.

Siamese network

The upper and lower neural networks have different input images, but have exactly the same parameters.

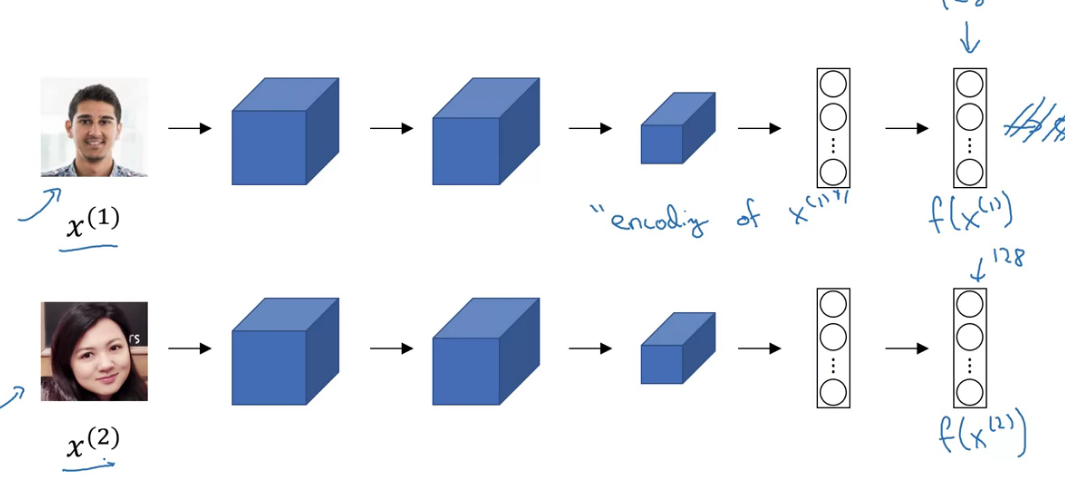
$$d(x^{(1)}, (x^{(2)}) = \Vert{f(x^{(1)}) -f(x^{(2)})}\Vert ^2_2$$

Parameters of NN define an encoding $f(x^{(i)})$
Learn parameters so that:
If $x^{(i)}, x^{(j)}$ are the same person, $ \Vert {f(x^{(1)}) -f(x^{(2)})} \Vert^2$ is small,
If $x^{(i)}, x^{(j)}$ are the same person, $ \Vert {f(x^{(1)}) -f(x^{(2)})} \Vert^2$ is large.

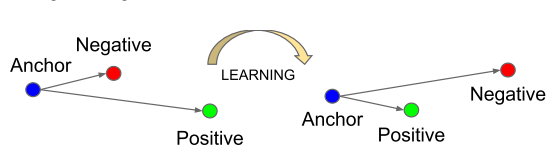
Triplet Loss

Triplet loss is an effective loss function for training a neural network to learn an encoding of a face image.
Training will use triplets of images $(A, P, N)$:

• A is an “Anchor” image–a picture of a person.
• P is a “Positive” image–a picture of the same person as the Anchor image.
• N is a “Negative” image–a picture of a different person than the Anchor image.
  You’d like to make sure that an image $A^{(i)}$ of an individual is closer to the Positive $P^{(i)}$ than to the Negative image $N^{(i)}$) by at least a margin $\alpha$:

$$\Vert f\left(A^{(i)}\right) -f \left(P^{(i)}\right) \Vert_{2}^{2} \alpha< \Vert f \left(A^{(i)} \right) - f \left(N^{(i)}\right) \Vert_{2}^{2}$$

$$\Vert f(A) -f(P) \Vert^2 -\Vert f(A) - f(N)\Vert^2 + \alpha <= 0$$

$\alpha$ is here to enforce a margin between the positive and the negatives.

Given 3 images A, P, N, loss function:
$$L(A, P, N) = max(\Vert f(A) -f(P)\Vert^2 -\Vert f(A) - f(N)\Vert^2 + \alpha, 0)$$
$$J = \sum^m_{i=1} L(A^{(i)}, P^{(i)}, N^{(i)})$$
Or,
$$\mathcal{J} = \sum^{m}_{i=1} \large[ \small \underbrace{\mid \mid f(A^{(i)}) - f(P^{(i)}) \mid \mid_2^2}_\text{(1)} - \underbrace{\mid \mid f(A^{(i)}) - f(N^{(i)}) \mid \mid_2^2}_\text{(2)} + \alpha \large ] \small_+ \tag{3}$$
Here, the notation “$[z]_+$” is used to denote $max(z,0)$.

Note

• The term (1) is the squared distance between the anchor “A” and the positive “P” for a given triplet; you want this to be small.
• The term (2) is the squared distance between the anchor “A” and the negative “N” for a given triplet, you want this to be relatively large. It has a minus sign preceding it because minimizing the negative of the term is the same as maximizing that term.
• $\alpha$ is called the margin. It’s a hyperparameter that you pick manually. You’ll use $\alpha = 0.2$.

Choosing the triplets A, P, N
During training, if A, P, N are chosen randomly, $d(A, P) + \alpha <= d(A, N)$ is easily satisfied
solution: choose triplets that’re “hard” to train on
$$d(A, P) + \alpha \le d(A, N)$$
$$d(A, P) \approx d(A, N)$$

Here we want to ensure that an image $x^a_i$ (anchor) of a specific person is closer to all other images $x^p_i$ (positive) of the same person than it is to any image $x^n_i$ (negative) of any other person.

Face verification and binary classification

$$\hat{y} = \sigma (\sum^{128}_{k=1} w_k \vert f(x^{(i)})_k - f(x^{(j)})_k \vert + b) \ \text{or} \ (f(x^{(i)}) _k - f(x^{(j)}) _k)^2$$

Ways to improve

• Put more images of each person (under different lighting conditions, taken on different days, etc.) into the database. Then, given a new image, compare the new face to multiple pictures of the person. This would increase accuracy.
• Crop the images to contain just the face, and less of the “border” region around the face. This pre-processing removes some of the irrelevant pixels around the face, and also makes the algorithm more robust.

Reference

[1] Schroff, F., Kalenichenko, D. and Philbin, J., 2015. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 815-823).

[2] Deeplearning.ai, Convolutional Neural Networks