Foundations of convolutional neural networks - Class review
Last updated on:4 months ago
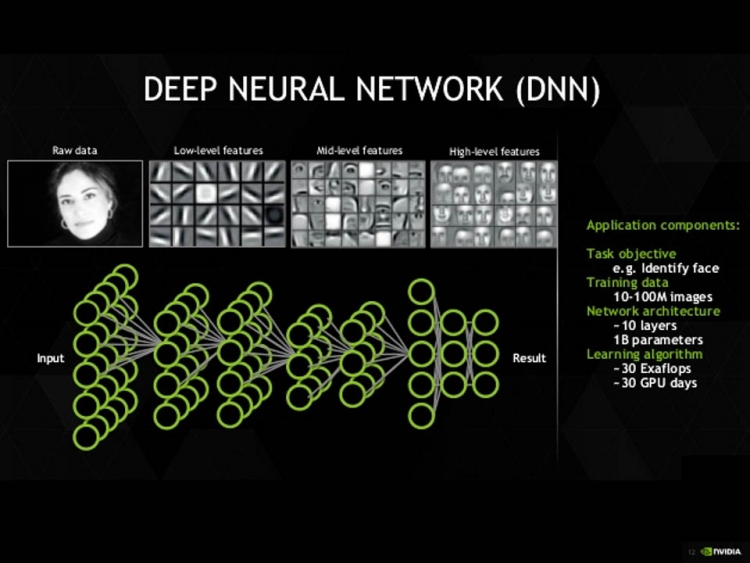
Convolutional neural networks are widely used in computer vision because it can help you compress your network system.
Computer Vision problems
CNNs (convolutional neural networks) allows abstracting an object’s identity or category from the specifics of the visual input (e.g., relative positions/orientation of the camera and the object).
image classification
object detection
neural style transfer
Directly modifying the output part of residual block would cause lower performance of the system, because skip connection has a fully copied tensor which could be interrupted by the not proper output design.
Edge detection example
Vertical edge detection
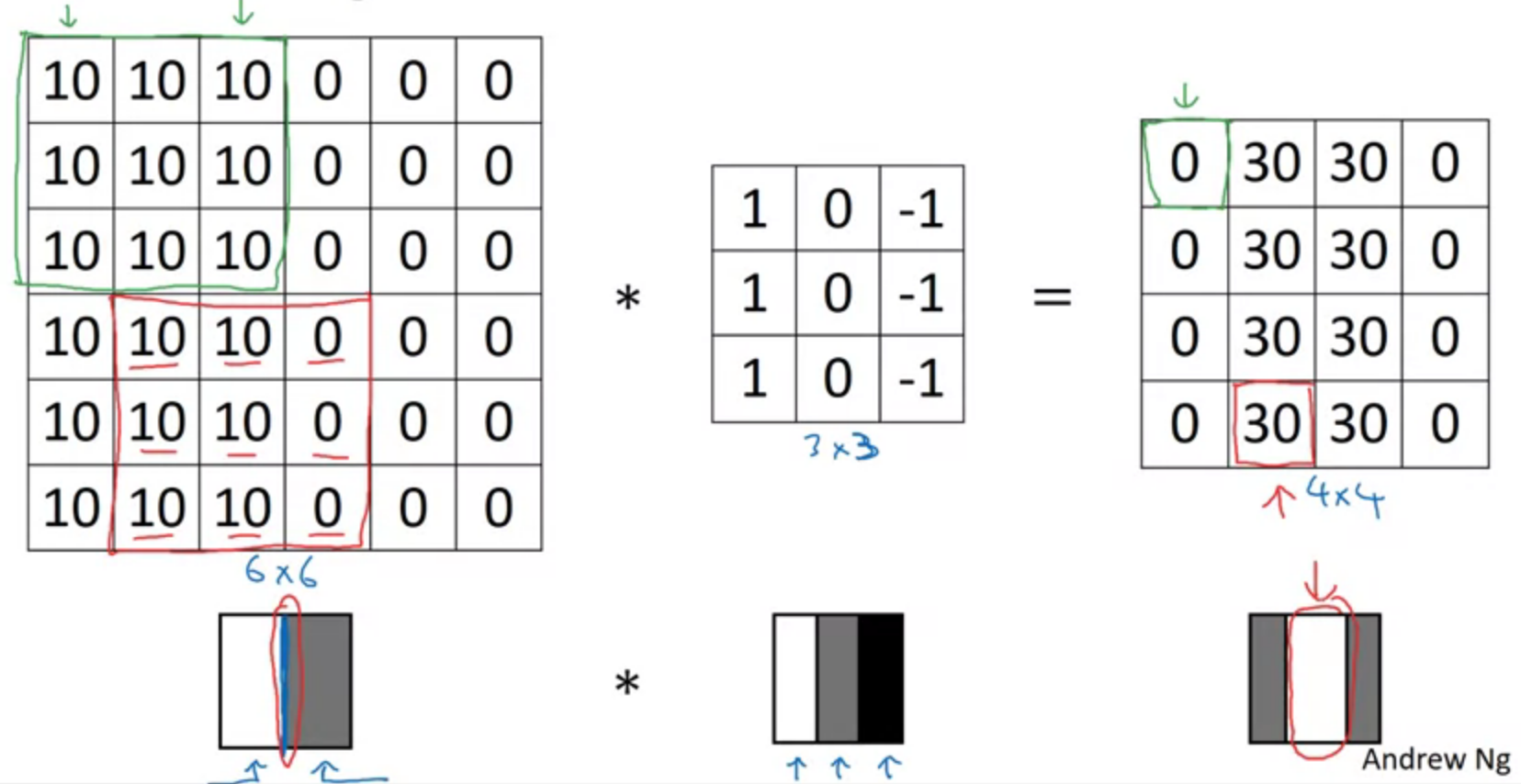
Learning to detect edges
Eg. horizontal, vertical, sobel, scharr filters.
Padding
Zero-padding adds zeros around the border of an image:
image, $$n \times n$$
filter, $$f \times f$$
image after convolution, $$(n-f+1) \times (n-f+1)$$
Valid convolution vs. same convolution
Valid convolution: no padding, $$n\times n * f\times f = (n - f + 1) * (n - f + 1)$$
Same convolution: pad so that output size is the same as the input size
$$n + 2p - f + 1 = n$$
means $$p = \frac{f - 1}{2}$$
$f$ is usually an odd number.
Same padding doesn’t change $n_H^{[l]}$ and $n_W^{[l]}$, while valid padding does. Pooling layers or valid padding can be used to downsize the height/width of the activation volumes. Sometimes they are helpful to build a deeper neural network.
Benefits
- Use a Conv layer without necessarily shrinking the height and width of the volumes
- Keep more of the information at the border of an images. Without padding, very few values at the next layer would be affected by pixels as the edges of an image
Problems
- shrink output
- throw away info from edge
Strided convolutions
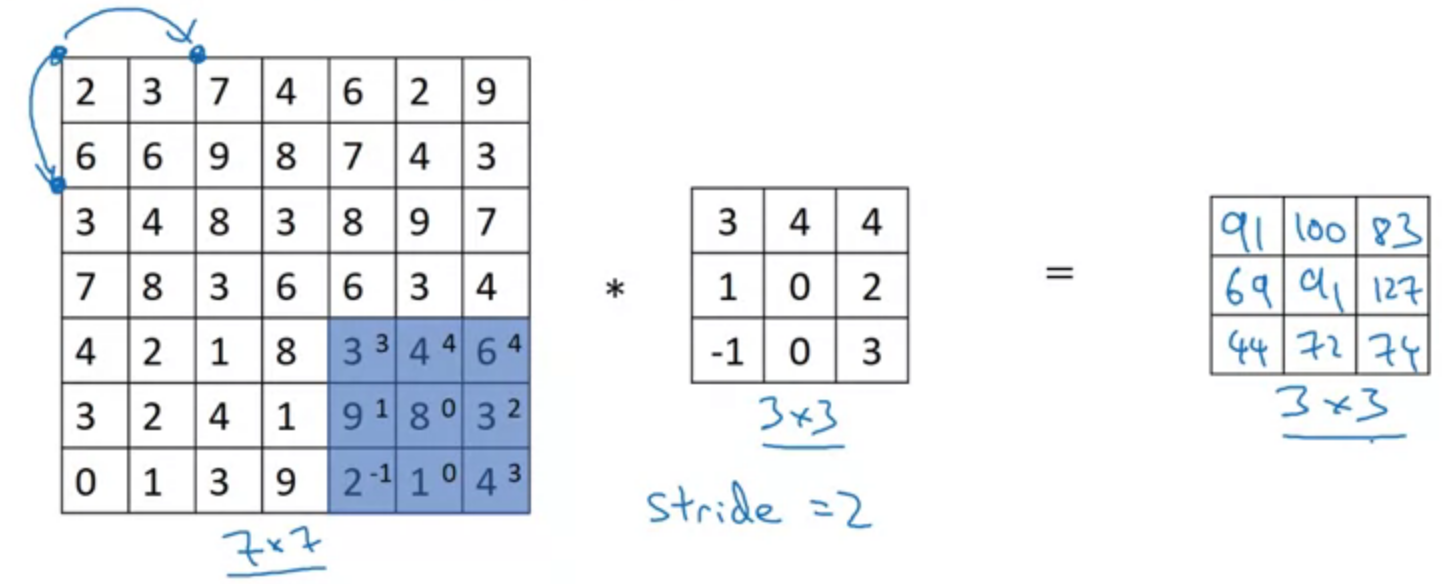
$$[z] = floor(z) $$
Dimension
$$\left[ \frac{n + 2p - f}{s} + 1 \right] \times \left[ \frac{n + 2p - f}{s} + 1 \right]$$
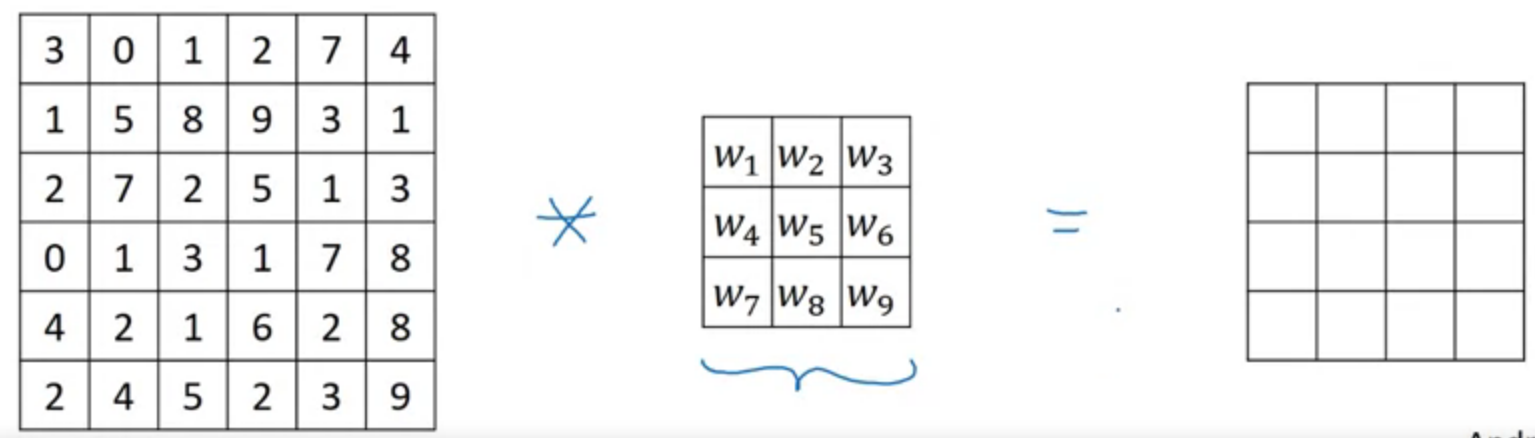
Convolution
Technical note on cross-correlation vs convolution
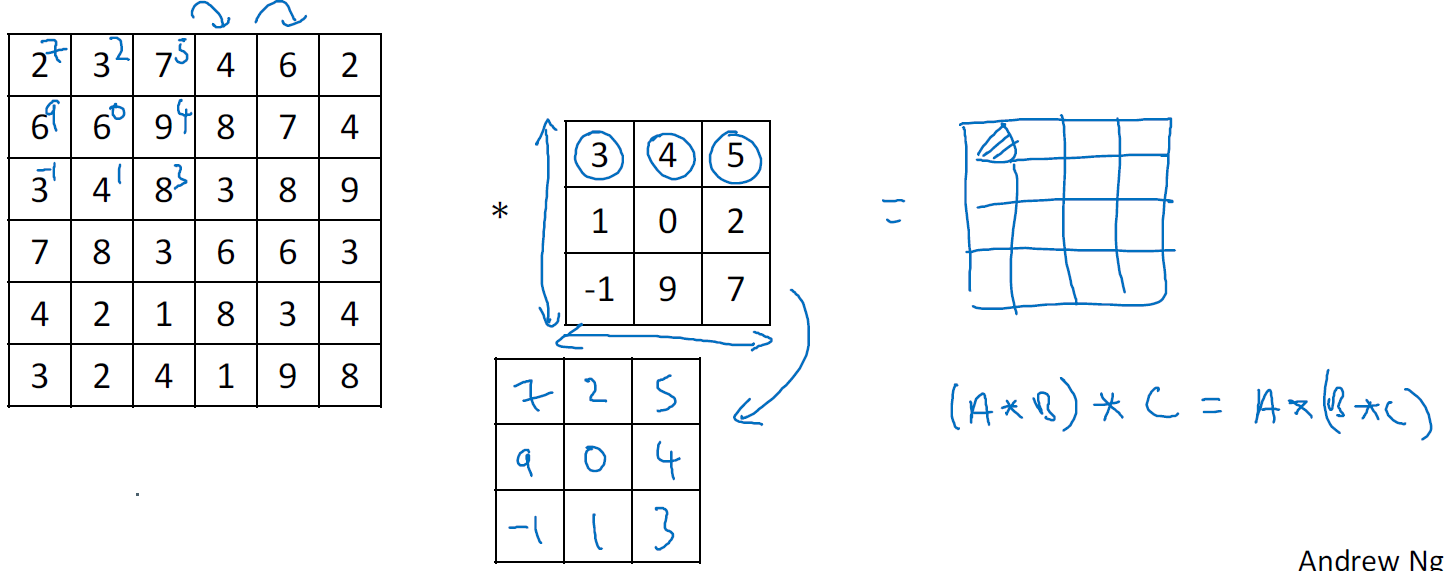
And it follows
$$(A*B)*C = A*(B*C)$$
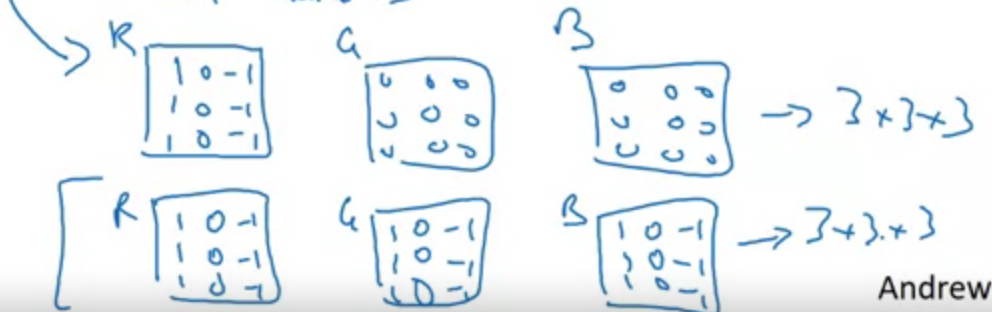
Convolutions on RGB images
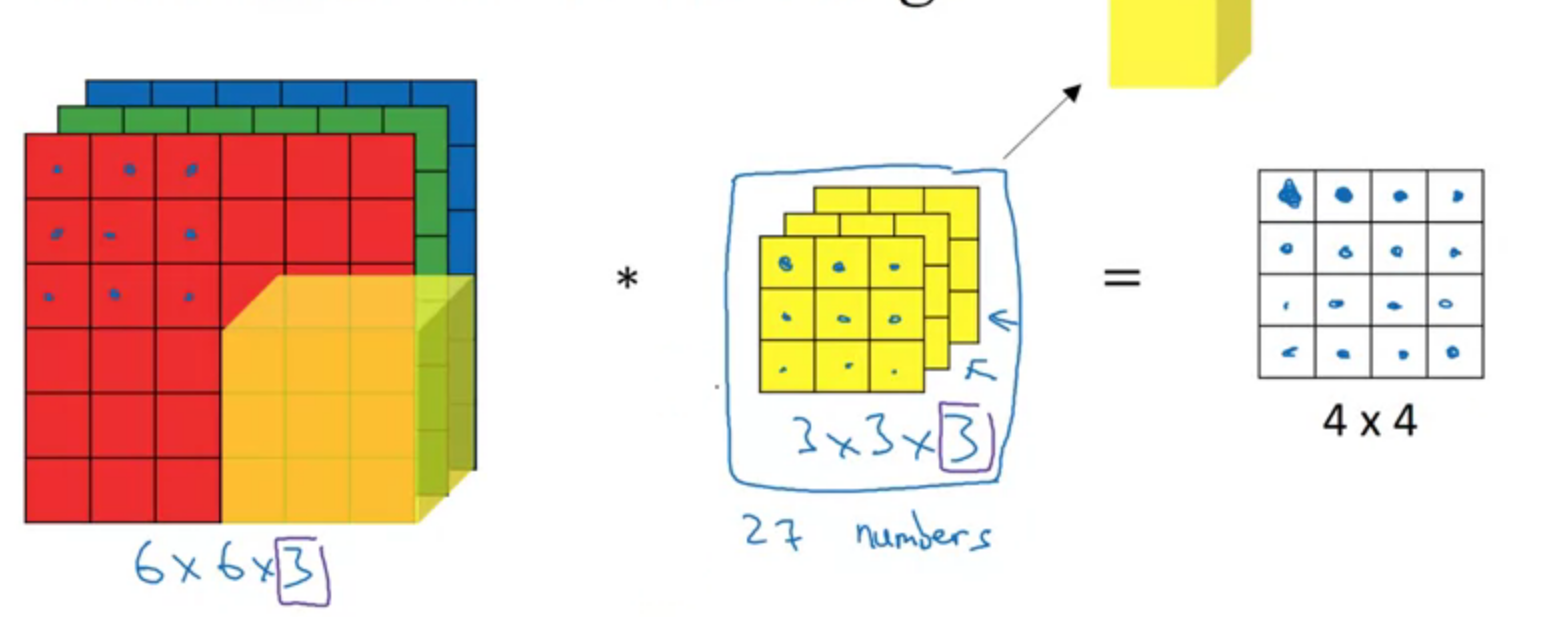
Detect edges only in R channel
Detect edges only in R, G and B channel
Multiple filters
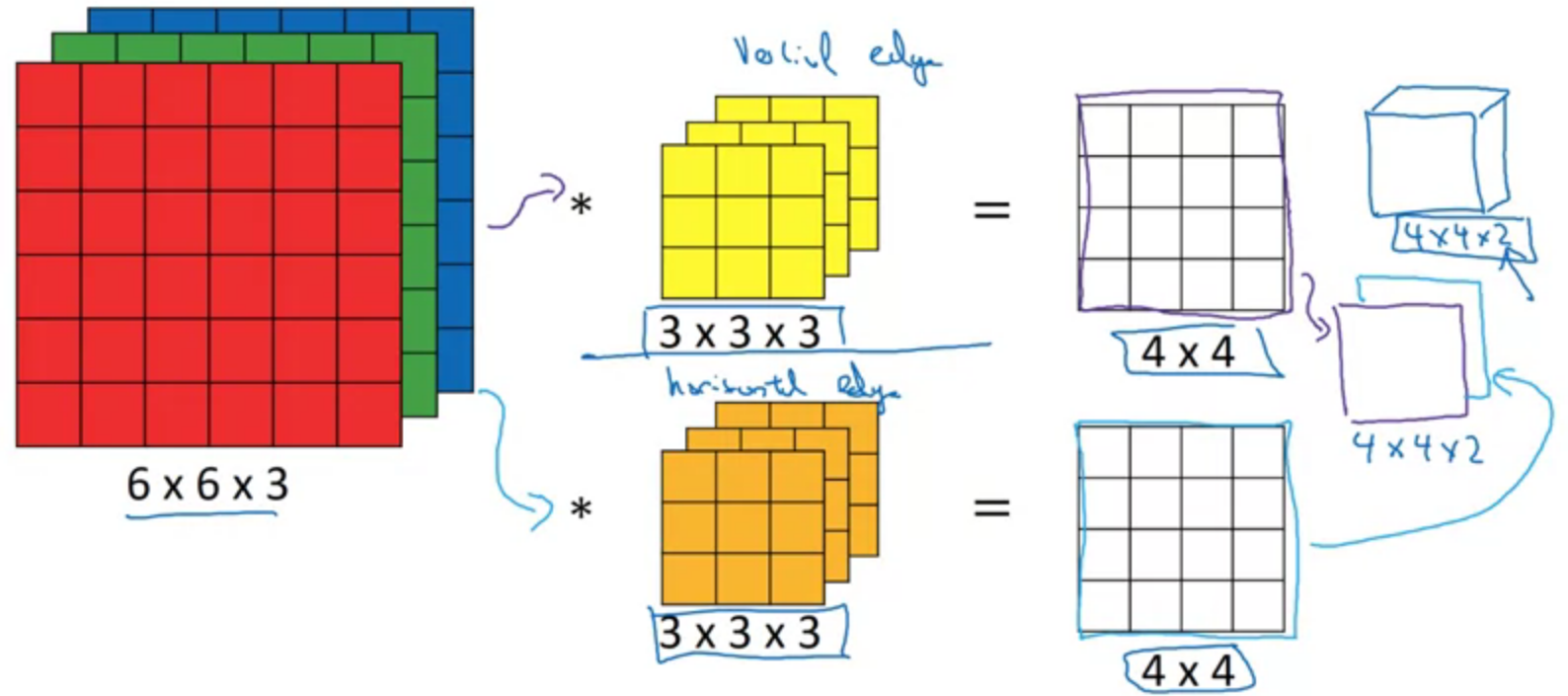
$$(n \times n \times n_c) * (f \times f \times n_c) \to (n - f +1) \times (n - f + 1) \times n_c^{‘}$$
$n_c^{‘}$ is number of filters.
One layer of a convolutional neural network
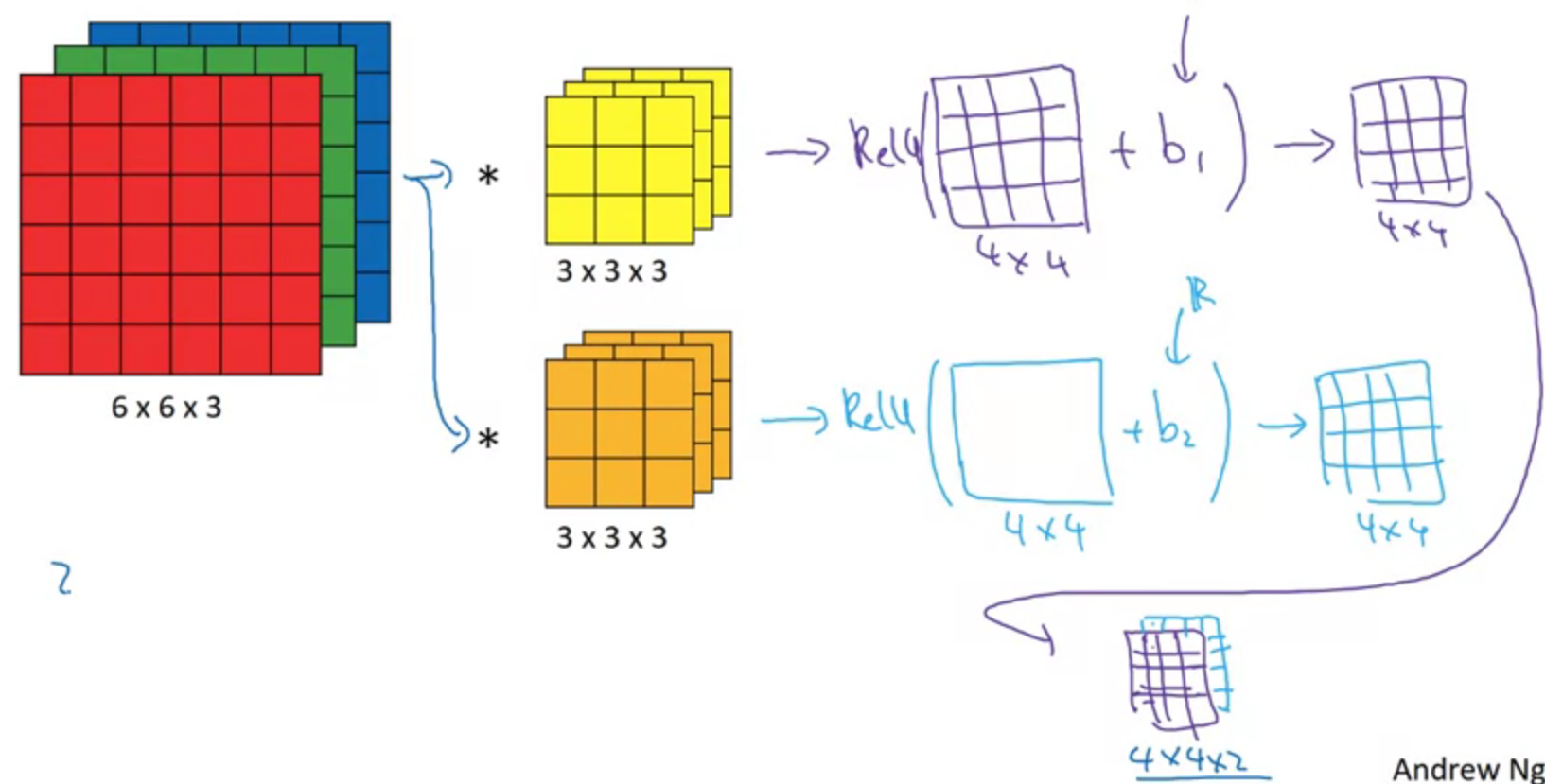
$$z^{[1]} = W^{[1]} a^{[0]} + b^{[1]}$$
$$a^{[1]} = g(z^{[1]})$$
The parameters number is not relevant to each image size.
Q&A: If you have 10 filters that are 3 x 3 x 3 in one layer of a neural network, how many parameters does that layer have?
$$3 \times 3 \times 3 = 27$$
Plus the parameter of bias,
$$27 + 1 = 28$$
With 10 filters, it would be
$$28 \times 10 = 280$$
Notation
$$f^{[l]} = \text{filter size}$$
$$p^{[l]} = \text{padding}$$
$$s^{[l]} = \text{stride}$$
$$n^{[l]}_c = \text{number of filters}$$
Each filter is: $$f^{[l]} \times f^{[l]} \times n^{[l - 1]}_c$$
Activations: $$a^{[l]} \to n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c$$
$$A^{[l]} \to m \times n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c$$
Weights: $$f^{[l]} \times f^{[l]} \times n^{[l - 1]}_c \times n^{[l]}_c$$
bias: $$(1, 1, 1, n^{[l]}_c)$$
Input: $$n^{[l - 1]}_H \times n^{[l - 1]}_W \times n^{[l - 1]}_c$$
Output: $$n^{[l]}_H \times n^{[l]}_W \times n^{[l]}_c$$
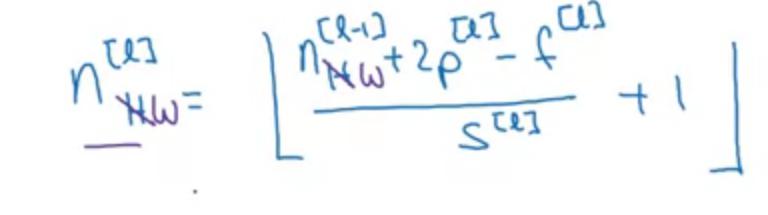
Group convolution
The grouped convolution means a group of convolutions for the layer, with multiple groups of kernels and corresponding multiple groups of output channels.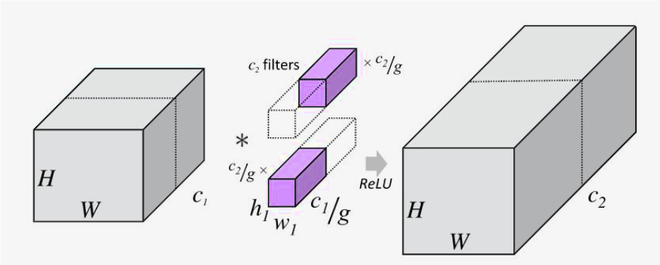
For example,
Conv = nn.Conv2d(
in_channels=100,
out_channels=5,
kernel_size=3,
stride=1,
padding=1,
groups=5)
print(conv.weight.shape)
> torch.Size([5, 20, 3, 3])Each kernel of the 5 filters will just use 20 input channels and create an output.
Lveaving $\text{groups}=1$ gives you torhc.Size([5, 100, 3, 3]), which means each filter will use all 100 input channels (vanilla convoltuion). Given that $\text{groups}=100$, it will have 100 filters and each filter handle one channel.
Example ConvNet
Height and width of images are gradually trending down while approaching in deeper layer. By contrast, the number of channels is increasing.

Types of layer in a convolutional network
- convolution (conv)
- pooling (pool)
- fully connected (FC)
Pooling layers
The function of pooling layers: To reduce variance, reduce computation complexity (as 2x2 max pooling/average pooling reduces 75% data) and extract low level features from neighbourhood.
Max pooling extracts the most important features like edges whereas, average pooling extracts features so smoothly.
Pooling stride each of the channel. 2D Pooling layer doesn’t not change the number of channels $n_c$.
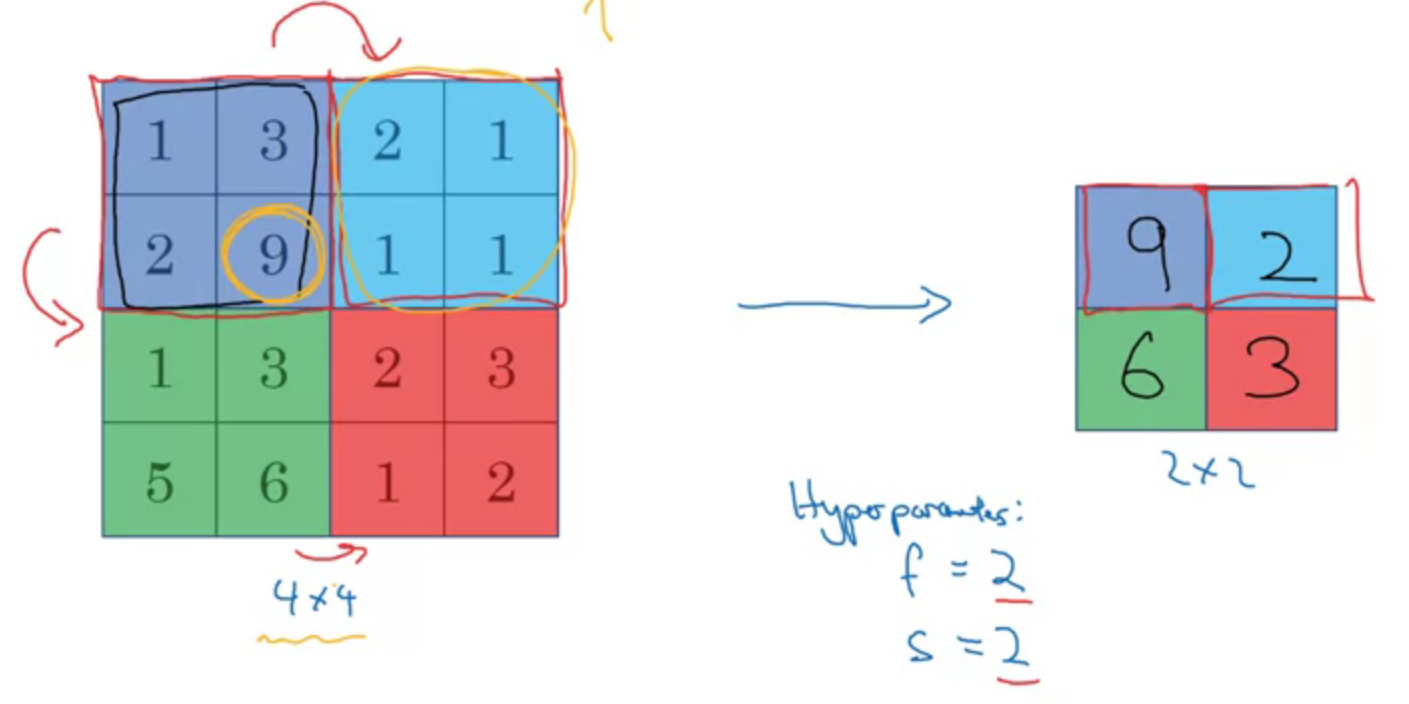
Max pooling
Average pooling
Get the average number of pooling region on each step.
Adaptive Average pooling
In Adaptive Pooling on the other hand, we specify the output size instead. And the stride and kernel-size are automatically selected to adapt to the needs. The following equations are used to calculate the value in the source code.
Stride = (input_size //output_size)
Kernel size = input_size - (output_size-1) * stride
Padding = 0Hyperparameters
f: filter size
s: stride
max or average pooling
no padding
$$f = 2, s = 2$$
$$\left[ \frac{n_H - f}{s} + 1 \times \frac{n_W - f}{s} + 1 \right] \times n_c$$
No parameter to learn.
Example
LeNet-5
Conv-pool-conv-pool-FC-FC-FC-Softmax
eg.
| Activation shape | Activation size | Parameters | |
|---|---|---|---|
| Input | (32,32,3) | 3072 | 0 |
| CONV1 (f=5, s=1) | (28,28,8) | 6272 | 608 |
| POOL1 | (14,14,8) | 1568 | 0 |
| CONV2 (f=5, s=1) | (10,10,16) | 1600 | 3216 |
| POOL2 | (5,5,16) | 400 | 0 |
| FC3 | (120,1) | 120 | 48120 |
| FC4 | (84,1) | 84 | 10164 |
| Softmax | (10,1) | 10 | 850 |
Calculus
For CONV, $$\text{No.} \text{parameters} = (f\times f + 1) \times n_c^{[l]}$$
For FC, $$\text{No.} \text{parameters} = (\text{activation size}_1 \times \text{activation size}_2) + \text{activation size}_2$$
Why convolutional neural network?
Parameter sharing: a feature detector (such as a vertical edge detector) that’s useful in one part of the image is probably useful in another part of the image.
Sparsity of connections: In each layer, each output value depends only on a small number of inputs.
translation variance
Putting it together
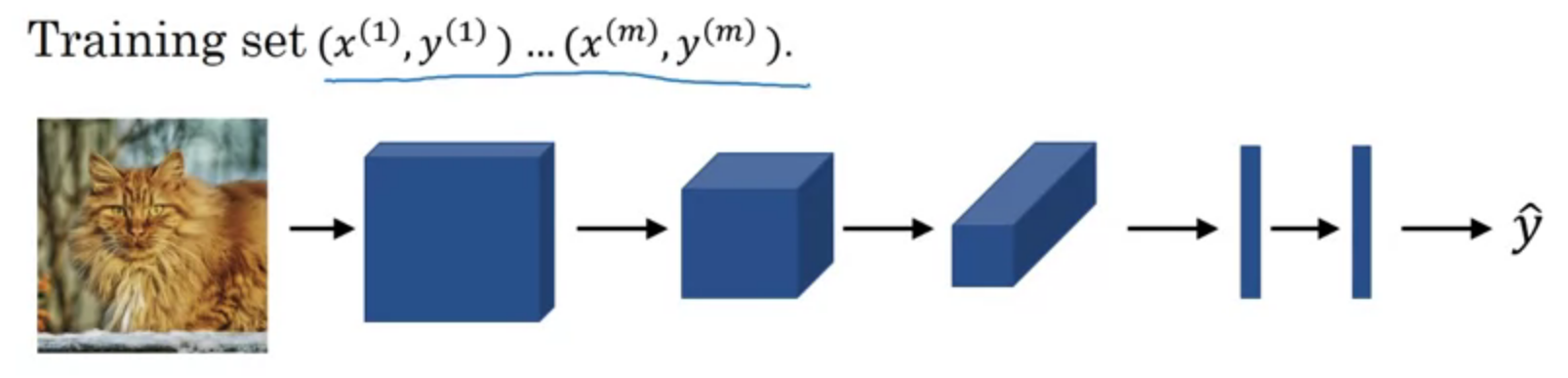
$$Cost\ J = \frac{1}{m} \sum^m_{i=1} L(\hat{y}^{(i)}, y^{(i)})$$
Use gradient descent to optimize parameters to reduce $J$.
Q&A
6.Suppose you have an input volume of dimension $n_H \times n_W \times n_C$. Which of the following statements you agree with? (Assume that “$1\times 1$ convolutional layer” below always uses a stride of 1 and no padding.)
You can use a 2D pooling layer to reduce $n_H$, $n_W$, and $n_C$.
-[x] You can use a 2D pooling layer to reduce $n_H$, $n_W$, but not $n_C$.
-[x] You can use a 1x1 convolutional layer to reduce $n_C$. but not $n_H$, $n_W$.
You can use a 1x1 convolutional layer to reduce $n_H$, $n_W$, and $n_C$.
Reference
[1] Voulodimos, A., Doulamis, N., Doulamis, A. and Protopapadakis, E., 2018. Deep learning for computer vision: A brief review. Computational intelligence and neuroscience, 2018.
[2] Deeplearning.ai, Convolutional Neural Networks
[3] What is the benefit of using average pooling rather than max pooling?
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!