Classic networks could be utilized in the first version of your own network. Let’s see how they looks like and how do we use them.

Classic networks

Very deep neural networks are difficult to train, because of vanishing and exploding gradient.

LeNet - 5

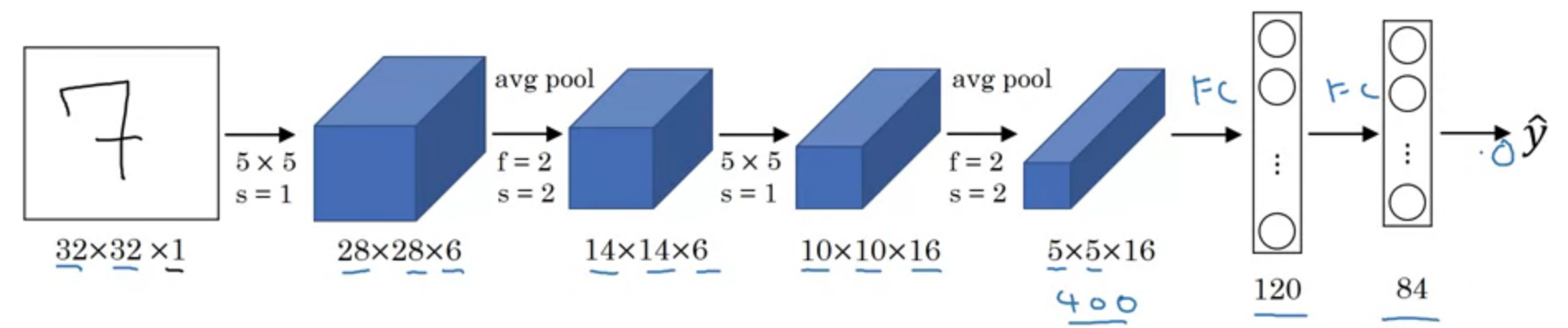
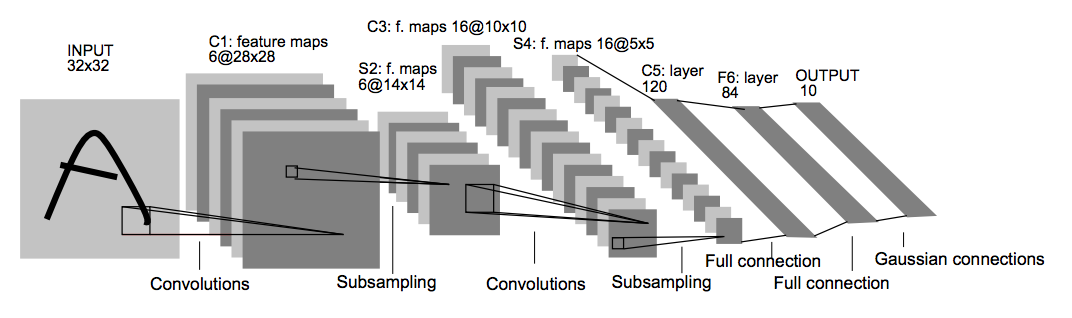
~60k parameters

Advanced: sigmoid/tanh, ReLU

AlexNet

AlexNet is proposed by Alex Krizhevsky et, al.. It has 60M parameters and 650M neurons, consists of five convolutional layers, some of which are followed by max-pooling layers, and three fully connected layers with a final 1000-way softmax.

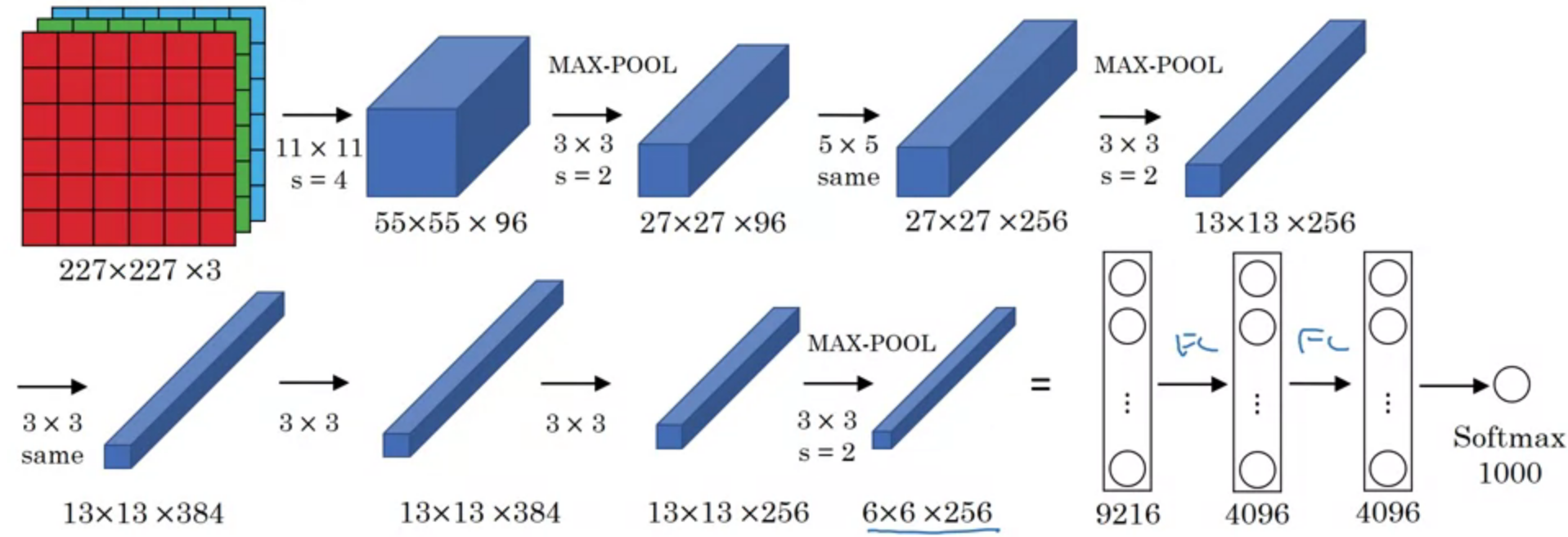
Similar to LeNet, but much bigger

ReLU, Multiple GPUs, Local response normalization (LRN) (doesn’t work well).

Why AlexNet?

The success of AlexNet is mostly attributed to its ability to leverage GPU for training and being able to train these huge numbers of parameters.

In the following layers, there were multiple improvements over AlexNet resulting in models like VGG, GoogleNet, and lately ResNet.

VGG-16

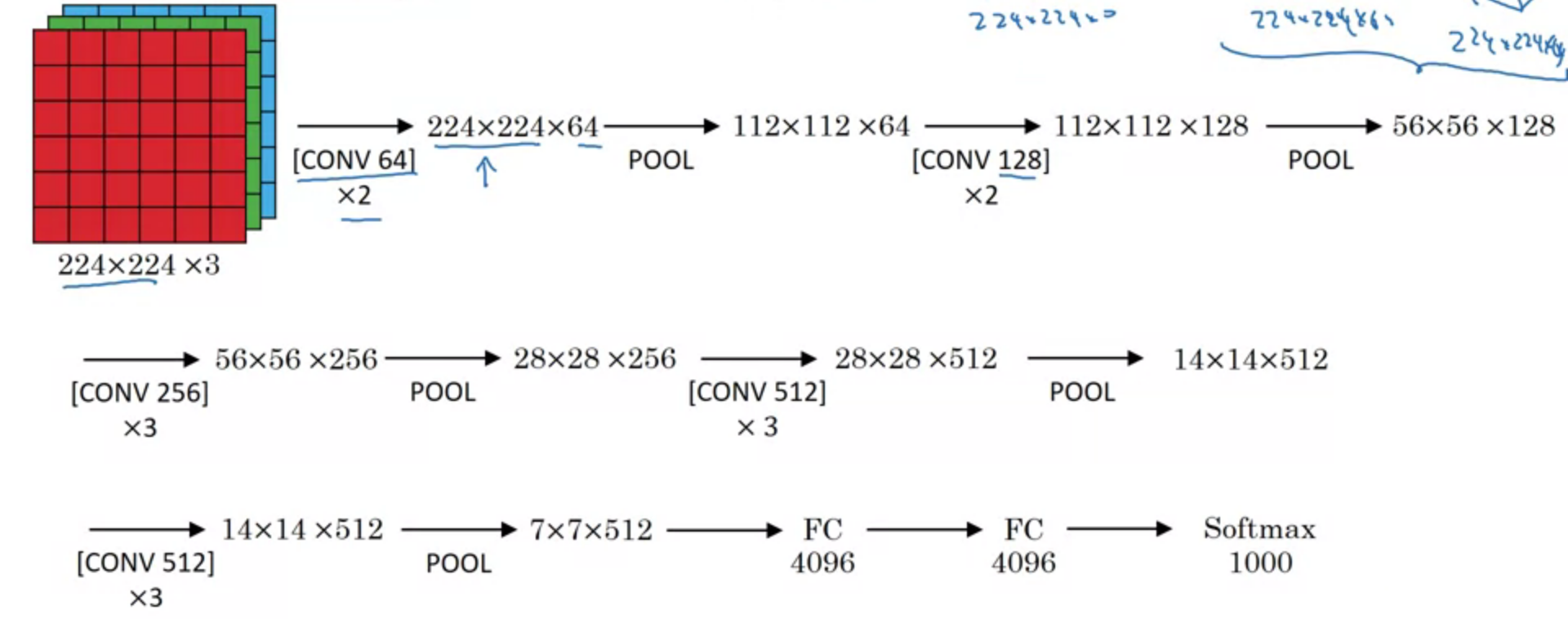
~138 M

Conv $3\times 3$ filter, $s = 1$, same
Max-pool $= 2\times 2, s = 2$

Residual Networks (ResNet)

Deeper neural networks are more difficult to train.

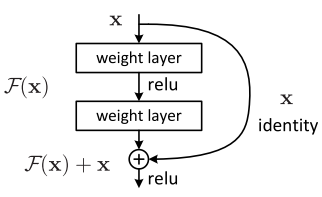
Residual block

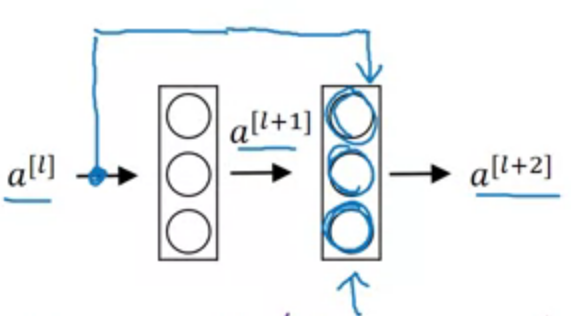
Skip connection

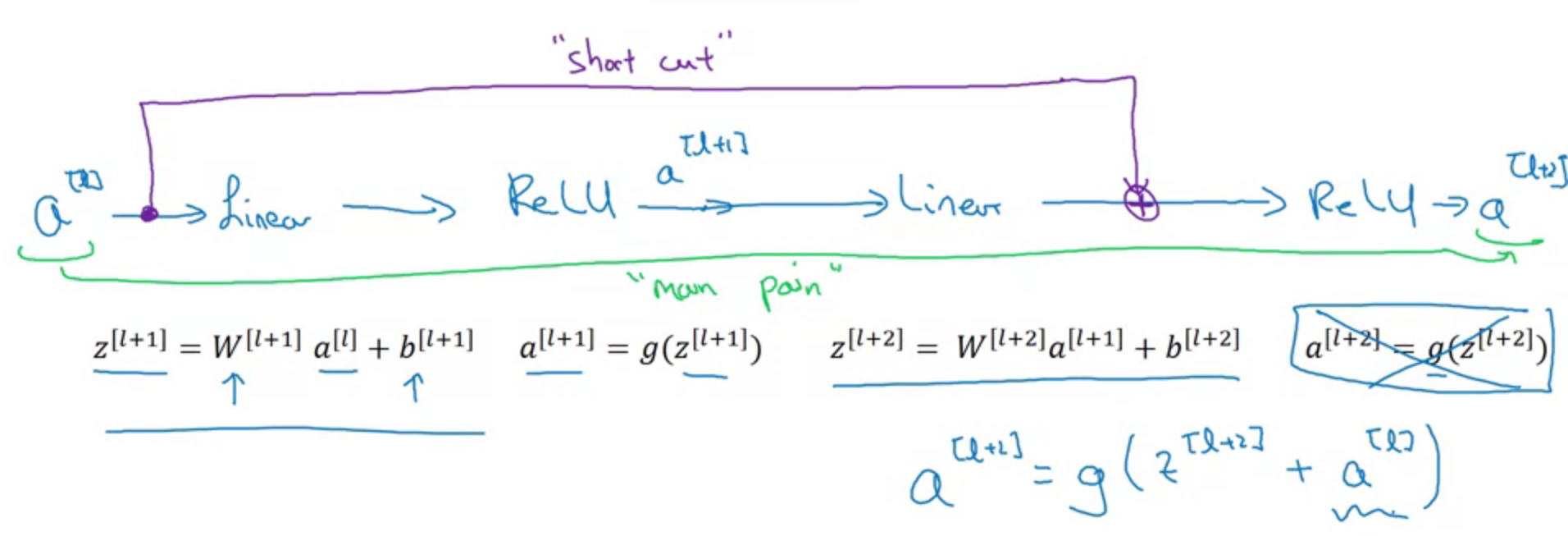
In ResNet, the formulation always learns residual functions; the identity shortcuts are never closed, and all information is always passed through, with additional residual functions to be learned.

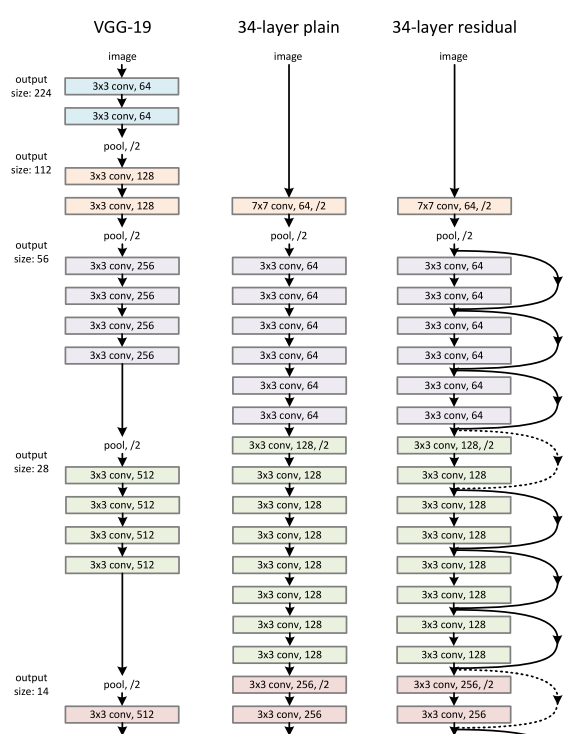
Architectures

Based on the above plain network, He et al. insert shortcut connections which turn the network into its counterpart residual version.

Why does ResNet work?

Identity function is easy for residual block to learn.

• The gradient descent gets to every layer, with only a small number if layers in between it needs to differentiate through.
• Each layer from the bottom of your stack of layers has a connection with the output layer that only goes through a couple of other layers, which means that the gradient is more pure.
• A way to solve the vanishing gradient, so that the model can be built deeper.

Q&A

5.Which ones of the following statements on Residual Networks are true? (Check all that apply.)

-[x] The skip-connection makes it easy for the network to learn an identity mapping between the input and the output within the ResNet block.

The skip-connections compute a complex non-linear function of the input to pass to a deeper layer in the network.

A ResNet with L layers would have on the order of $L^2$ skip connections in total.

-[x] Using a skip-connection helps the gradient to backpropagate and thus helps you to train deeper networks

Reference

[1] Krizhevsky, A., Sutskever, I. and Hinton, G.E., 2012. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems, 25, pp.1097-1105.

[2] AlexNet: The First CNN to win Image Net

[3] He, K., Zhang, X., Ren, S. and Sun, J., 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).

[4] Why do residual networks work?

[5] Deeplearning.ai, Convolutional Neural Networks