Once you have constructed your learning system, you have to tune its hyperparameters. The number of set of parameters means how many models you should train.

Tuning process

• Hyperparameters: $\alpha, \beta, \varepsilon$.
• Layers
• Hidden units
• Learning rate decay
• Mini-batch size

Try random value

Don’t use a grid. Picking hyperparameters at random. Grid search can be used for the number of hidden units and layers.

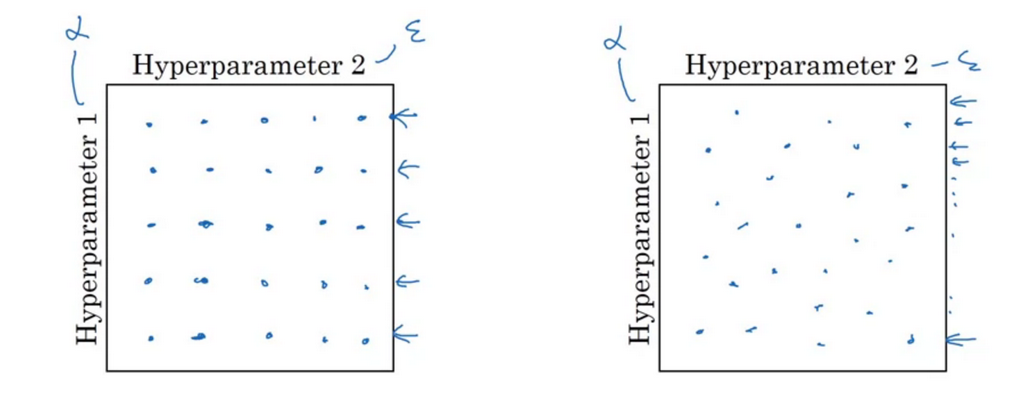
Coarse to fine

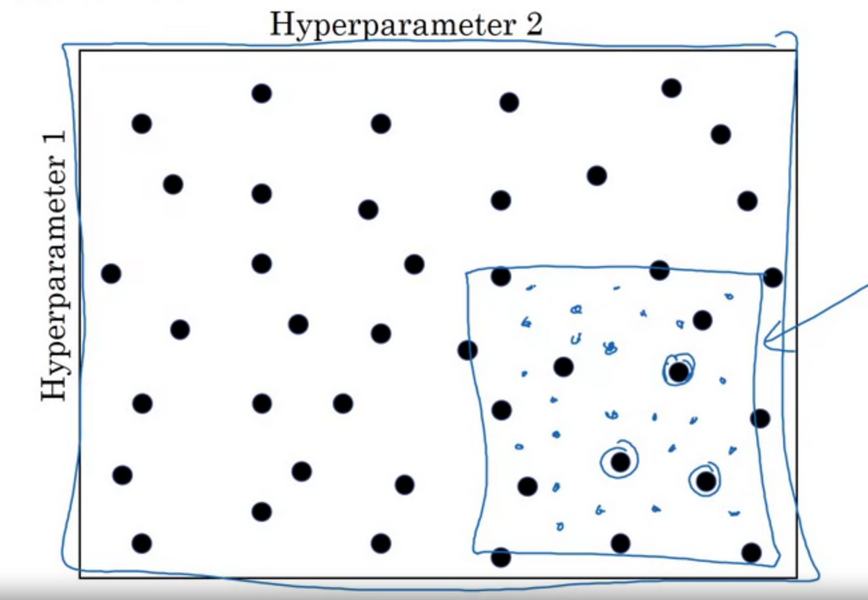
Using an appropriate scale

Appropriate scale for hyperparameters

$$r = -4 * np.random.rand()$$
$$\alpha = np.power(10, r)$$

Exponentially weighted averages, don’t choose it in linear scale

$$choose 1 - \beta$$
$$1 - \beta = 10^r$$
$$\beta = 1 - 10^r$$

It is more sensitive to change $\beta$ when it is close to 1.

$\beta = $	0.9	…	0.999
	10		1000
$1-\beta =$	0.1	…	0.001

$$\beta: (0.9000 \to 0.9005) ~10$$

$$\beta: (0.999) ~ 1000 \to (0.9995) ~ 2000$$

Hyperparameters tuning in practice: Pandas vs. Caviar

Intuition does get scale, re-evaluate occasionally.

• Babysitting one model, Panda
• Training many models in parallel, Caviar

Normalizing activations in a network

Normalizing inputs to speed up learning, batch norm
$$z^{(i)}_{norm} = \frac{z^{(i)} - \mu}{\sigma^2 + \varepsilon}$$

$$\tilde{z}^{(i)} = \gamma z^{(i)}_{\text{norm}} + \beta$$

If $\gamma = \sqrt(\sigma^2 + \varepsilon)$
$\beta = \mu$

then, $\tilde{z}^{(i)} =z^{(i)}$

Why does batch norm work?

• Learning on shifting input distribution

• Batch norm: no matter how it changes, it eliminates the amount of updating parameters in the earlier layer that can affect the distribution of values.

• The earlier layer doesn’t change much, has the same mean and variance

• Reduce the problem of input value changing, this value becomes more stable

Batch norm at test time
$\mu, \sigma^2$: estimate using exponentially weighted average (across mini-batches)

$$X^1, X^2, X^3, …$$

$$\mu^{1}[l]$$

Using data from training set.

Fitting batch norm into a neural network

$$\beta^{[l]} = \beta^{[l]} - \alpha d\beta^{[l]}$$

Working with mini-batches

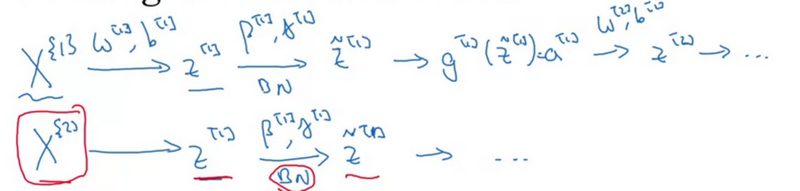
Mean subtraction will get rid of the constant.

Parameters:

$$\omega ^{[l]}, \cancel{b^{[l]}}, \beta ^{[l]}, \gamma ^{[l]}$$

$$z ^{[l]} = \omega ^{[l]} a^{[l - 1]} + \cancel{b^{[l]}}$$

Softmax

Multi-class classification
Softmax layer

$$ Z^{[L]} = W^{[L]} a^{[L-1]} + b^{[L]} $$

Activation function

$$ t = exp(z^{[L]}) $$

$$a^{[L]} = \frac {exp(z^{[L]})} {\sum^4_{i=1} t_i}$$

Training a softmax classifier
Hardmax $[1 0 0 0]^T$
Softmax, more gentle mapping
Softmax regression generalizes logistic regression to C classes.
Loss function
$$L(\hat{y}, y) = - \sum^4_{j=1} y_j \log \hat{y}_j$$
Cost function

$$J(\omega^{[1]}, b^{[1]}, …) = \frac{1}{m} \sum^m_{i=1} L(\hat{y}, y)$$

$$Y = [y^{(1)}, y^{(2)}, …, y^{(l)}]$$
$$\hat{Y} = [\hat{y}^{(1)}, \hat{y}^{(2)}, …, \hat{y}^{(l)}]$$

Reference

[1] Deeplearning.ai, Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization