After you implement your first simple learning model, you can try to enhance its performance by following optimization algorithms.

Mini-batch gradient descent

See Large Scale Machine Learning - Class Review.

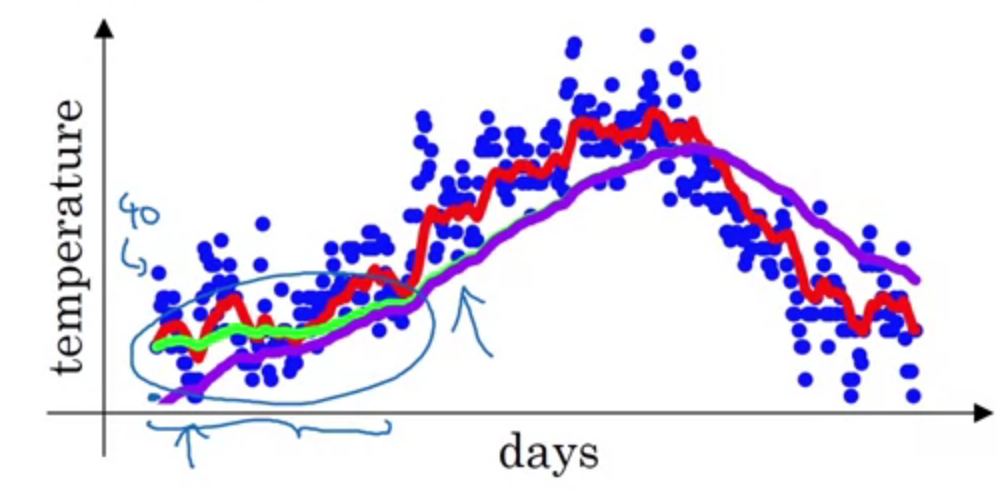
Exponentially weighted averages

The exponentially weighted (moving) averages (EWMA) is a statistic with the characteristic that it gives less and less weight to data as they get older and older.

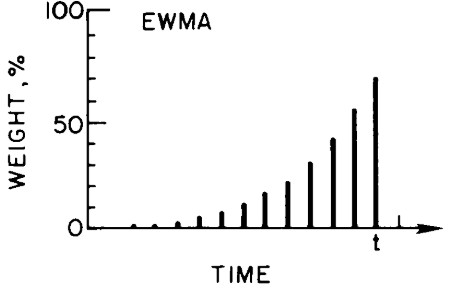
$$v_t = \beta v_t-1 + (1-\beta) \theta_t$$
v(previous values)
Implementing it
$$v_\theta := 0$$
$$v_\theta := \beta v + (1-\beta) \theta_1$$
…
$$v_\theta := \beta v_\theta + (1-\beta) \theta_t$$
$$(1 - \varepsilon)^{1\varepsilon} = 1/e$$

Bias correction in exponentially weighted averages

In practice, don’t be bothered. Without bias correction, your model can also work well after considerable training epochs.

$$\frac{v_t}{1-\beta^t}$$

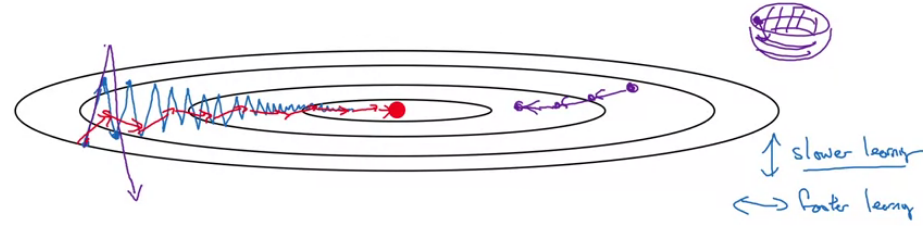
Gradient descent with Momentum

On iteration t:
compute $dW, db$ on current mini-batch,
Version 1 (recommended)
$$v_{dW} = \beta_1 v_{dW} + (1 - \beta_1) dW$$
$$v_{db} = \beta_1 v_{db} + (1 - \beta_1) db$$
Version 2
$$v_{dW} = \beta_1 v_{dW} + dW$$
$$v_{db} = \beta_1 v_{db} + db$$
Learning rate will be very different between the two methods.

$$W:= W - \alpha v_{dW}, b:= b - \alpha v_{db}$$

Ball shape function
$\beta v_{dW}, \beta v_{db}$, velocity
$dW, db$, acceleration

Hyperparameters choice:

Hyperparameters: $\alpha, \beta$
Common value: $\beta = 0.9$

The larger the momentum $\beta$ is, the smoother the update because the more we take the past gradients into account. But if $\beta$ is too big, it could also smooth out the updates too much.

RMSprop

On iteration t:
compute $dW, db$ on current mini-batch,
$$s_{dW} = \beta_2 s_{dW} + (1 - \beta_2) dW.^2$$, element-wise
$$s_{db} = \beta_2 s_{db} + (1 - \beta_2) db.^2$$
$$W:= W - \alpha \frac{s_{dW}}{\sqrt{s_{dW}} + \varepsilon}, b:= b - \alpha \frac{s_{db}}{\sqrt{s_{db}} + \varepsilon}$$

Hyperparameters choice:

$\sqrt{s_{dW}}$ and $\sqrt{s_{db}}$ are close to 0, so plus $\varepsilon$, maybe $10^{-8}$

$\beta_2: 0.999$ (default it)
$\varepsilon: 10^{-8}$ (default it)

$\beta_2$ infinitesimally close to 1 would lead to infinitely large bias, and infinitely large parameter updates.

Adam optimization algorithm

Adam: adaptive moment estimation
Momentum + RMSprop + Bias correction
On iteration t:
compute $dW, db$ on current mini-batch,

$$v_{dW} = \beta_1 v_{dW} + (1 - \beta_1) dW$$

$$v_{db} = \beta_1 v_{db} + (1 - \beta_1) db$$

$$s_{dW} = \beta_2 s_{dW} + (1 - \beta_2) dW.^2 (\text{element-wise})$$

$$s_{db} = \beta_2 s_{db} + (1 - \beta_2) db.^2$$

$$V^{\text{corrected}}_{dW} = V_{dW}/(1-\beta_1^t)$$

$$V^{\text{corrected}}_{db} = V_{db}/(1-\beta_1^t)$$

$$S^{\text{corrected}}_{dW} = V_{dW}/(1-\beta_2^t),$$

$$S^{\text{corrected}}_{db} = S_{db}/(1-\beta_2^t)$$

$$W:= W-\alpha \frac{V^{\text{corrected}}_{dW}} {\sqrt{S^{corrected}_{dW}}}+ \varepsilon$$

$$b:= b-\alpha \frac{V^{\text{corrected}}_{db}} {\sqrt{S^{corrected}_{db}} + \varepsilon}$$

Hyperparameters choice:
$\alpha$: needs to be tune
$\beta_1: 0.9$ (default it)
$\beta_2: 0.999$ (default it)
$\varepsilon: 10^{-8}$ (default it)

Learning rate decay

When gradient descent nears a minima in the cost surface, the parameter values can oscillate back and forth around the minima. One method to prevent this is to slow down the parameter updates by decreasing the learning rate.

But someone also proposed that by increasing the learning rate $\alpha$ and scaling the batch size $m\propto \alpha$, the model can reach equivalent test accuracies after the same number of training epochs. And one can increase the momentum coefficient $\beta_1$ and scale $m \propto 1/(1 - m)$.

1 epoch = 1 pass through dataset

$$\alpha = \frac{1}{1+\text{decayRate}\times \text{epochNum}} \alpha_0$$
Other learning rate decay methods
$$\alpha = 0.95^{\text{epochNum}} \alpha_0, \ \text{Exponentially decay}$$
$$\alpha = \frac{k}{\text{epochNum}} \alpha_0 \ \text{or} \ \frac{k}{\sqrt{t}} \alpha_0$$

Discrete staircase

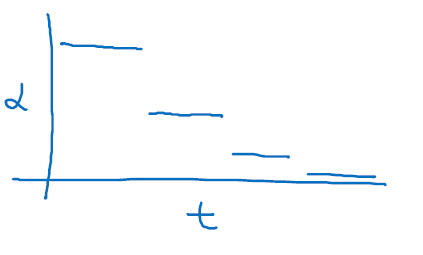
Manual decay works when you are training a small number of models

Problem of plateaus

• Unlikely to get stuck in a bad local optima
• Plateaus can make the learning slow

Adam move down the plateaus, get rid of plateaus.

epoch

An epoch is defined as the number of times an algorithm visits the data set .In other words, epoch is one backward and one forward pass for all the training.

Iteration is defined as the number of times a batch of data has passed through the algorithm. In other words, it is the number of passes, one pass consists of one forward and one backward pass.

For example- Consider a set of 1000 images having a batch size of 10 and each iteration would process 10 images, it will take100 such iterations to complete 1 epoch

Reference

[1] Deeplearning.ai, Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization

[2] Hunter, J.S., 1986. The exponentially weighted moving average. Journal of quality technology, 18(4), pp.203-210.

[3] Zeiler, M.D., 2012. Adadelta: an adaptive learning rate method. arXiv preprint arXiv:1212.5701.

[4] Smith, S.L., Kindermans, P.J., Ying, C. and Le, Q.V., 2017. Don’t decay the learning rate, increase the batch size. arXiv preprint arXiv:1711.00489.

[5] Epoch vs Iteration when training neural networks?

[6] Kingma, D.P. and Ba, J., 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.