Weight Initialization Methods - Class review
Last updated on:3 years ago
A well chose initialization of filter weights can speed up your learning systems. I want to make a summary of some advanced weight initialization methods in this blog.
What is Initialization?
When you train your learning systems, you should first set the parameters of the systems. Better values of parameters can later be obtained by updating.
A well-chosen initialization can:
Speed up the convergence of gradient descent
Increase the odds of gradient descent converging to a lower training (and generalization) error
Initializing weights to very large random values does not work well.
Zeros initialization
Zeros initialization means you initialize your learning systems rate with 0 value, which is harmful, which leads to network failing break symmetry and $n^{[l]} = 1$.
Symmetry breaking
A phenomenon in which (infinitesimally) small fluctuations acting on a system crossing a critical point decide the systems’ fate, by determining which branch of a bifurcation is taken.
Random initialization
Gaussian distributions initialization
$$Var[W^i] = \sigma^2$$
$$W\sim \mathcal{N} (0, \sigma^2)$$
N means normal distribution.
Advantages
- Symmetry is broken so long as $W^{[l]}$ is initialized randomly.
Shortcoming
- As the result of fixed standard deviations, very deep models (> 8 conv layers) have difficulties to converge.
Xavier initialization
$$Var[W^i] = \frac{2}{n_i + n_{i+1}}$$
$$W\sim U[-\frac{\sqrt{6}}{\sqrt{n_j + n_{j+1}}}, \frac{\sqrt{6}}{\sqrt{n_j + n_{j+1}}}]$$
U means continuous uniform distribution.
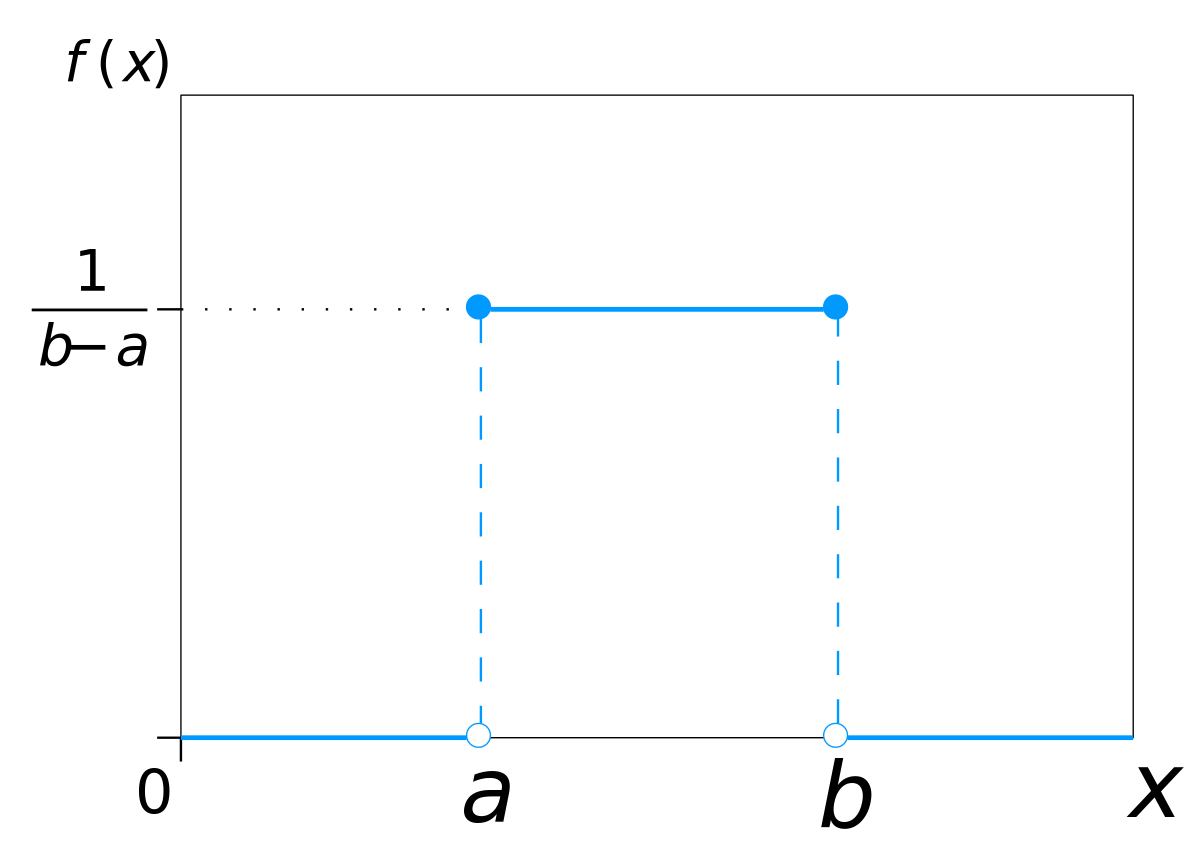
$$f(n) =
\begin{cases}
\frac{1}{b-a}, & \text{for $a\leq x\leq b$} \\ 0, & \text{for $x<a$ or $x>b$}
\end{cases}$$
He initialization
$$Var[W^i] =\sqrt{\frac{2}{n_l}}$$
$$W\sim \mathcal{N} (0, \sqrt{\frac{2}{n_l}})$$
Multiply $\sqrt{\frac{2}{layers-dims[l - 1]}}$ when initializing $W^{[l]}$
Xavier initialization vs. He initialization
The former is for linear activation functions only, but the latter is also valid by taking ReLU/PReLU into account.
Reference
[1] Deeplearning.ai, Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization
[2] He, K., Zhang, X., Ren, S. and Sun, J., 2015. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE international conference on computer vision (pp. 1026-1034).
[3] Glorot, X. and Bengio, Y., 2010, March. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the thirteenth international conference on artificial intelligence and statistics (pp. 249-256). JMLR Workshop and Conference Proceedings.
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!