Last updated on：5 days ago

As a researcher in deep learning, we have to make use of metrics to measure our models’ performance. I’ll introduce the most seen metrics in this blog.

Error matrices

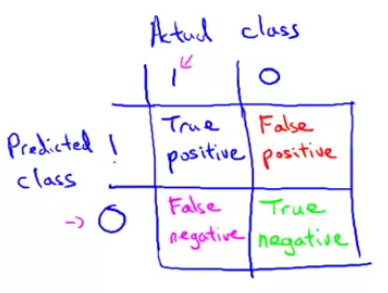
Positive and negative are your judgement result. True or False means your judgement is right or wrong.

Condition positive (P): the number of real positive cases in the data.
Condition negative (N): the number of real negative cases in the data.
True positive (TP): a test result that correctly indicates the presence of a condition or characteristic.
True negative (TN): a test result that correctly indicates the absence of a condition or characteristic.
False positve (FP), type I error: a test result which wrongly indicates that a particular condition or attribute is present.
False negative (FN), type II error: a test result which wrongly indicates that a particular condition or attribute is absent.

Divisor P, N means all positive or negative cases

Accuracy = (true positives + true negatives) / (total examples)
Precision = (true positives) / (true positives + false positives)
Recall (or Sensitivity) = (true positives) / (true positives + false negatives)
F1 score (F score) = $2\frac{PR}{P+R}$ or $\frac{2}{1/P+1/R}$
Specificity = $\frac{TN}{TN + FP}$

Biomedical meaning

Specificity: Find the healthy guys from all people, not giving miseading message.
Sensitivity: Find the illness guys from all people, giving the timely message.

$F_{\beta }$ score

Emphase the sensitivity, by giving large $\beta$ value.
$${\displaystyle F_{\beta }=(1+\beta ^{2})\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{(\beta ^{2}\cdot \mathrm {precision} )+\mathrm {recall} }}}$$

For instance, if $\beta = 2$, then $F_{2}$ score would be:
$${\displaystyle F_{\beta }=5\cdot {\frac {\mathrm {precision} \cdot \mathrm {recall} }{(4\cdot \mathrm {precision} )+\mathrm {recall} }}}$$

Metrics Rate

Rate means the proportion of an indicator. The fraction of metrics rate is depended on the rate name.

Rate name	Denominator	Numerator	Formula
True positive rate/TPR	TP + FN	TP	$\frac{TP}{TP + FN}$
False positive rate/FPR	FP + TN	FP	$\frac{FP}{FP + TN}$
True negative rate/TNR	TN + FP	TN	$\frac{TN}{TN + FP}$
False negative rate/FNR	FN + TP	FN	$\frac{FN}{FN + TP}$

Denominator is the total of the rate name situation in judgement (positive or negative). For instance, True positive means ground truth and judgement are right. We get all positive judgement item, that is TP $+$ FN. Meanwhile, the numerator is the rate name itself. True positive is TP.

The ground truth and judgement are both different in two rate name means we can sum up them to 1.

$$\text{FPR} + \text{TNR} = 1$$

$$\text{TPR} + \text{FNR} = 1$$

Name

TPR: Sensitivity, Recall

FPR: Fall out

TNR: Specificity, selectivity

FNR: Miss rate

ROC

A receiver operating characteristic curve, or ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied.

ROC curve is TPR-FPR curve, which means that we need to compute TPR and FPR first.

AUC is area under curve. It can be obtained by calculate the area among ROC curve, $x$ axis, and $y = 1$ axis.

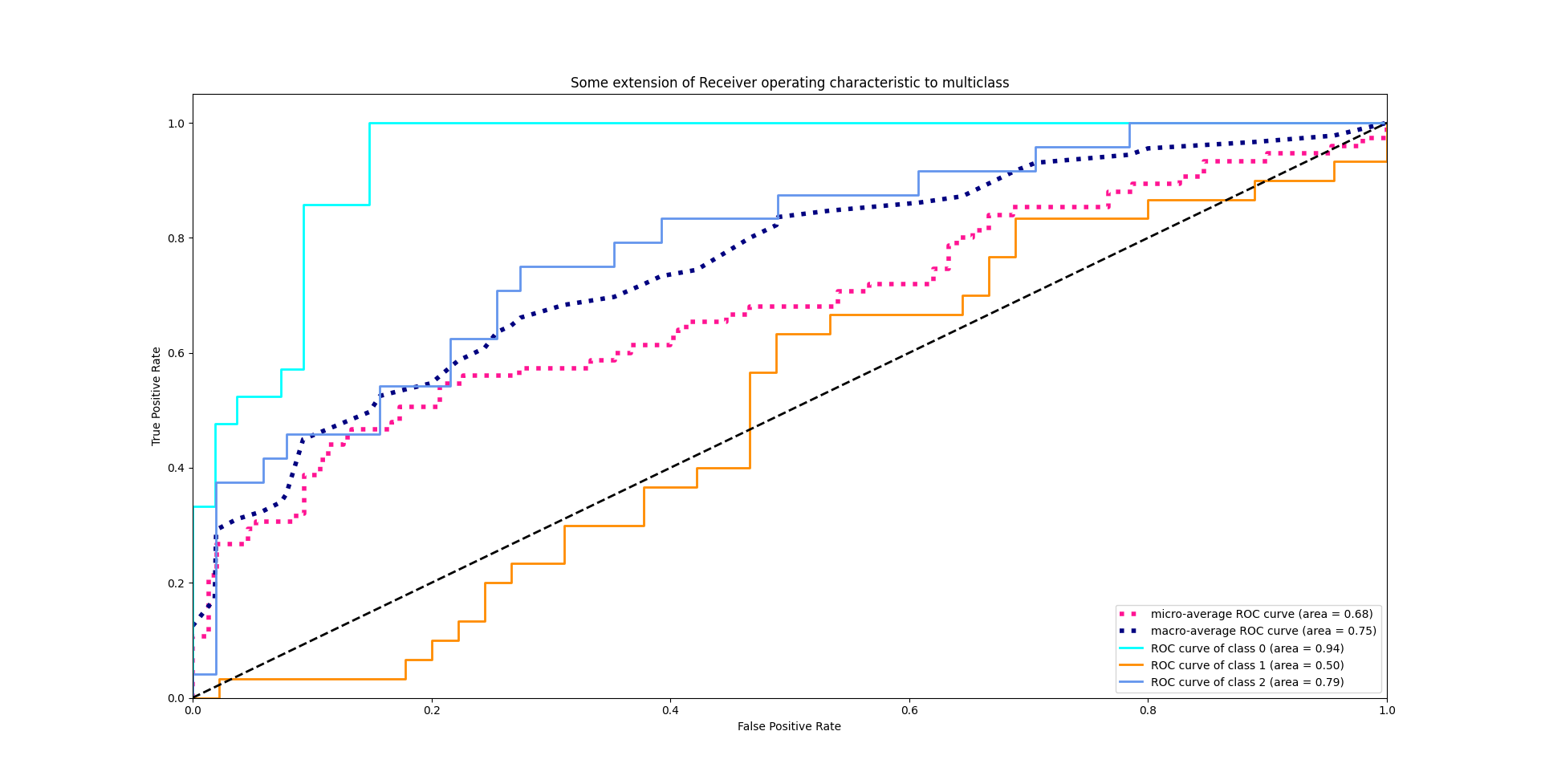
I guess you may have a question about plotting a curve. We get the TPR and FPR result in evaluating process, which can just be plotted in one point. How do we plot this curve? Actually, we need to set a threshold to define how large possibility is taken as a positive judgement.

For multi classes, we plot each class ROC one by one. First binarize the other class and the interested class, then take it as a two class curve plotting problem.

from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
import numpy as np
from sklearn import metrics


y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])

fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)

>>> fpr
array([ 0. ,  0.5,  0.5,  1. ])
>>> tpr
array([ 0.5,  0.5,  1. ,  1. ])
>>> thresholds
array([ 0.8 ,  0.4 ,  0.35,  0.1 ])

auc = metrics.auc(fpr, tpr)
>>> auc
0.75


plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()