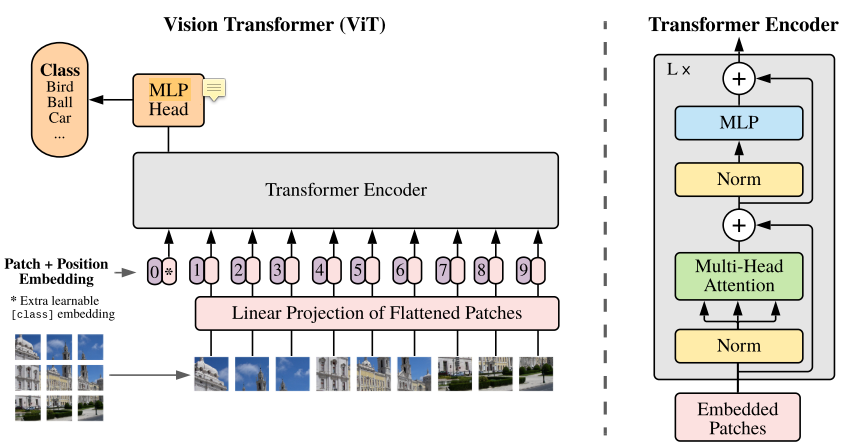
Vision transformer slices the image into patches and uses self-attention mechanisms (inter-patches) (qkv interaction) to process the features.

Vision transformer

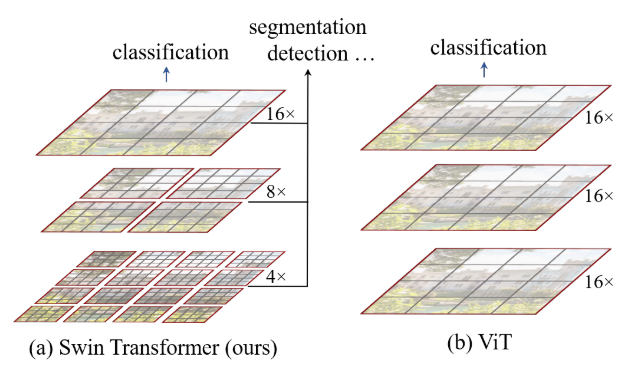
Swin transformer

Shifted window transformer. Merging image patches (shown in gray) in deeper layers. Linear computation complexity to input image size due to computation of self-attention only within each local window (shown in red).

SwinTransformer:
    x = self.PatchEmbed(x)
    if self.ape:
        x = x + self.absolute_pos_embed
    x = self.pos_drop(x)
    for layer in self.layers:
        x = layer(x)
    x = self.norm(x)  # B L C
    x = self.avgpool(x.transpose(1, 2))  # B C 1
    x = torch.flatten(x, 1)

    x = self.Classifier(x)
# BasicLayer
# SwinTransformerBlock + Patch merging

Cyclic shift + partition windows + window attention + merge window + reverse cyclic shift + FFN:

SwinTransformerBlock:
    # cyclic shift
    if self.shift_size > 0:
        shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
    else:
        shifted_x = x
    # partition windows
    x_windows = windowPartition(shifted_x, self.window_size)  # nW*B, window_size, window_size, C
    x_windows = x_windows.view(-1, self.window_size * self.window_size, C)  # nW*B, window_size*window_size, C
    # W-MSA/SW-MSA
    attn_windows = self.attn(x_windows, mask=self.attn_mask)  # nW*B, window_size*window_size, C
    # merge windows
    attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
    shifted_x = windowReverse(attn_windows, self.window_size, H, W)  # B H' W' C
    # reverse cyclic shift
    if self.shift_size > 0:
        x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
    else:
        x = shifted_x
    x = x.view(B, H * W, C)
    # FFN
    x = shortcut + self.drop_path(x)
    x = x + self.drop_path(self.mlp(self.norm2(x)))

Shifted window:
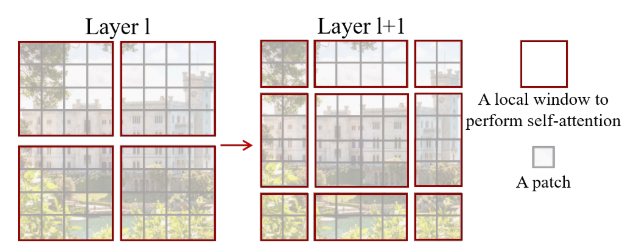
For crossing the boundary, change the size of windows (通過變換窗口大小達到cross boundary的效果).
Layer l: self-attention is computed within each window
Layer l+1: self-attention computation in the new windows crosses the boundaries of the previous windows in layer l, providing connections among them

h_slices = (slice(0, -self.WindowSize),
                        slice(-self.WindowSize, -self.shift_size),
                        slice(-self.shift_size, None))
w_slices = (slice(0, -self.WindowSize),
            slice(-self.WindowSize, -self.shift_size),
            slice(-self.shift_size, None))

Patch merging:

# input
torch.Size([3, 3136, 96])
# split image res
torch.Size([3, 56, 56, 96])
# downsize image res into 4 channel
torch.Size([3, 28, 28, 384])
# merge image res
torch.Size([3, 784, 384])
# reduction
torch.Size([3, 784, 192])

windowPartition: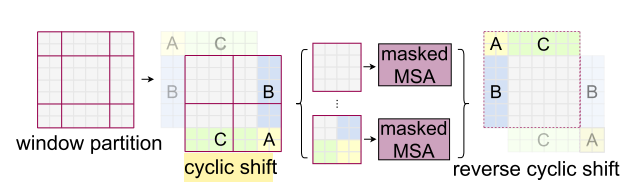

# Input
torch.Size([1, 56, 56, 1])
# PatchesRes split into 4
torch.Size([1, 8, 7, 8, 7, 1])
# Window
torch.Size([64, 7, 7, 1])
# (num_windows*B, WindowSize, WindowSize, C)

windowReverse:

# windows.shape
torch.Size([192, 7, 7, 96])
# Split num_ win * B into batchsize and two  H // window size 
torch.Size([3, 8, 8, 7, 7, 96])
# merge window size and  H // window size into PatchesRes
torch.Size([3, 56, 56, 96])

QKV

196 is the number of patches, 768 is the patches ensemble size, Q K V directly handles this tensor.
Original:

x.shape
torch.Size([3, 3, 224, 224])
Patch embedding:
x.shape
torch.Size([32, 197, 768])

Dimension of q, k, v is the same:

Query.shape
torch.Size([32, 12, 197, 64])
Key.shape
torch.Size([32, 12, 197, 64])
Value.shape
torch.Size([32, 12, 197, 64])
x.shape
torch.Size([32, 12, 197, 197])

Token

An additional [class] token (image representation).
It is not really important. However, we wanted the model to be “exactly Transformer, but on image patches,” so we kept this design from Transformer, where a token is always used.

x.shape
torch.Size([3, 196, 768])
ClassTokens.shape
torch.Size([3, 1, 768])
x.shape
torch.Size([3, 197, 768])

Token classes are common practice in NLP where you have one token that pools information from the rest of the tokens through rounds of attention, usually to classify the sentence at the end. Whether it is completely necessary for ViT to work is up for debate. My take is it isn’t that important. You could pool all the embeddings from the last layer and probably still get great results at scale.

In the field of AI, a token is a fundamental unit of data that is processed by algorithms, especially in natural language processing (NLP) and machine learning services.
A token is essentially a component of a larger data set, which may represent words, characters, or phrases.

Oxford:
A round piece of metal or plastic used instead of money to operate some machines or as a form of payment.

A piece of paper that you pay for and that somebody can exchange for something in a shop.

Tokenization

Tokenization breaks text into smaller parts for easier machine analysis, helping machines understand human language.
These tokens can be as small as characters or as long as words. The primary reason this process matters is that it helps machines understand human language by breaking it down into bite-sized pieces, which are easier to analyze.

MLP layer

A multilayer perceptron (MLP) is a feedforward artificial neural network (ANN) class. The term MLP is used ambiguously, sometimes loosely to mean any feedforward ANN, sometimes strictly to refer to networks composed of multiple layers of perceptrons (with threshold activation); see § Terminology. Multilayer perceptrons are sometimes colloquially referred to as “vanilla” neural networks, especially when they have a single hidden layer.
An MLP consists of at least three layers of nodes: an input layer, a hidden layer, and an output layer.

Transformer 的 MLP：兩層linear

self.fc1 = nn.Linear(in_features, hidden_features)
self.act = act_layer()
self.fc2 = nn.Linear(hidden_features, out_features)
self.drop = nn.Dropout(drop)

Latent space

Laten space is a set of items within a manifold (pipe shape with openings) in which items “resembling each other are positioned closer” to one another in the latent space.
Position within the latent space can be viewed as being defined by a set of latent variables that emerge from the resemblances from the objects.

Data structure

Input: reshape the image $x \in R^{H\times W\times C}$ into a sequence of flattened 2D patches $x_p \in R^{N \times (P^2 \dot C)}$.
$(P, P)$ is the resolution of each image patch.
$N = HW/P^2$ is the number of patches
Patch embedding: image to patch, 224x224 to 16 x 16
Position embedding: 3 dimensions to 2 dimensions (+1 dimension if in batch)

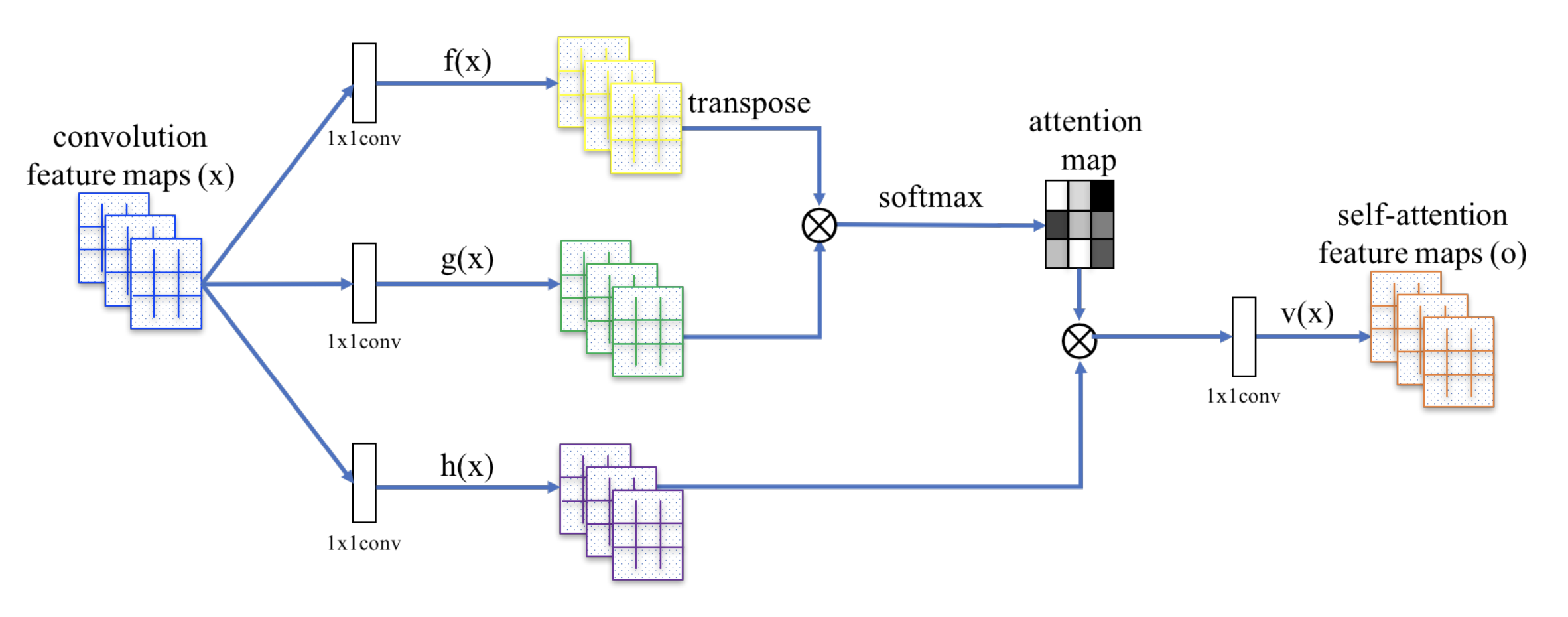
Shortcoming

It doesn’t work well for a small dataset without pretrained in the large dataset (ImageNet 1k):
E.g., mobilenetv3 large got 0.89 accuracy, but efficientvitxs got 0.58 accuracy in epoch 70 - 90

1. Make your modifications to the ViT encoder, then pretrain your new architecture using IN1k, then fine-tune with Oxford pets. This is very compute intensive, but considering you are already getting good results on a standard ViT using this transfer approach, then I’d play it safe and use this.
2. If you happen to have a lot of unlabelled samples that are closer to the target dataset than IN1k (let’s say ~100,000-10,000,000 images of animals), you can use self-supervised pre-training then transfer the parameters to the downstream classification task. DINO, MAE, and SimMIM are all pretty popular approaches for self-supervised learning. Again, this is going to be pretty compute intensive but if you want to avoid using IN1k data this is probably your best bet.
3. Use a CNN instead of ViT. ViTs are nice and fancy but for most applications where the number of training samples in the downstream (target) dataset is limited then a well-trained off-the-shelf CNN like ResNet/EfficientNet is probably a better approach.

Why

The hand wavy explanation for ViT needing so many data is because they basically need to learn inductive bias towards images from nothing, so a lot of training epochs are spent to just learn the inductive bias.

Inductive bias

The inductive bias is restricting your hypothesis space to a centain class of hypothesis.
It could be a set of assumptions that the learner uses to predict outputs of given inputs that it has not encountered.

Oxford:
Using particular facts and examples to form general rules and principles. (归纳)

ViT vs. CNN on inductive bias

The difference in inductive bias between ViTs and CNNs stems from their architectural design and the assumptions they make about the data.

CNNs assume spatial locality (nearby pixels are related) and hierarchical structures (complex patterns are built from simpler ones).

ViTs don’t assume spatial locality and hierarchical structures in images.
Instead, they rely on learning patterns by dividing images into patches and treating these patches as tokens in a sequence.

ViTs are treated as low-pass filters, emphasising shapes and curvature.
CNNs can function as both low-pass (large kernel) and high-pass (small kernel) filters.

CNN vs ViT classification and segmentation head

For classification,

# CNN
x.shape
torch.Size([4, 512, 1, 1])

x.shape
torch.Size([4, 512])

x.shape
torch.Size([4, 8])

# ViT
x.shape
torch.Size([4, 768])

x.shape
torch.Size([4, 8])

Segmentation can use it directly.
The segmentation head can just be those only connected to the final layers since there is no dimension change for ViT during its encoding process.
Similar to UNet.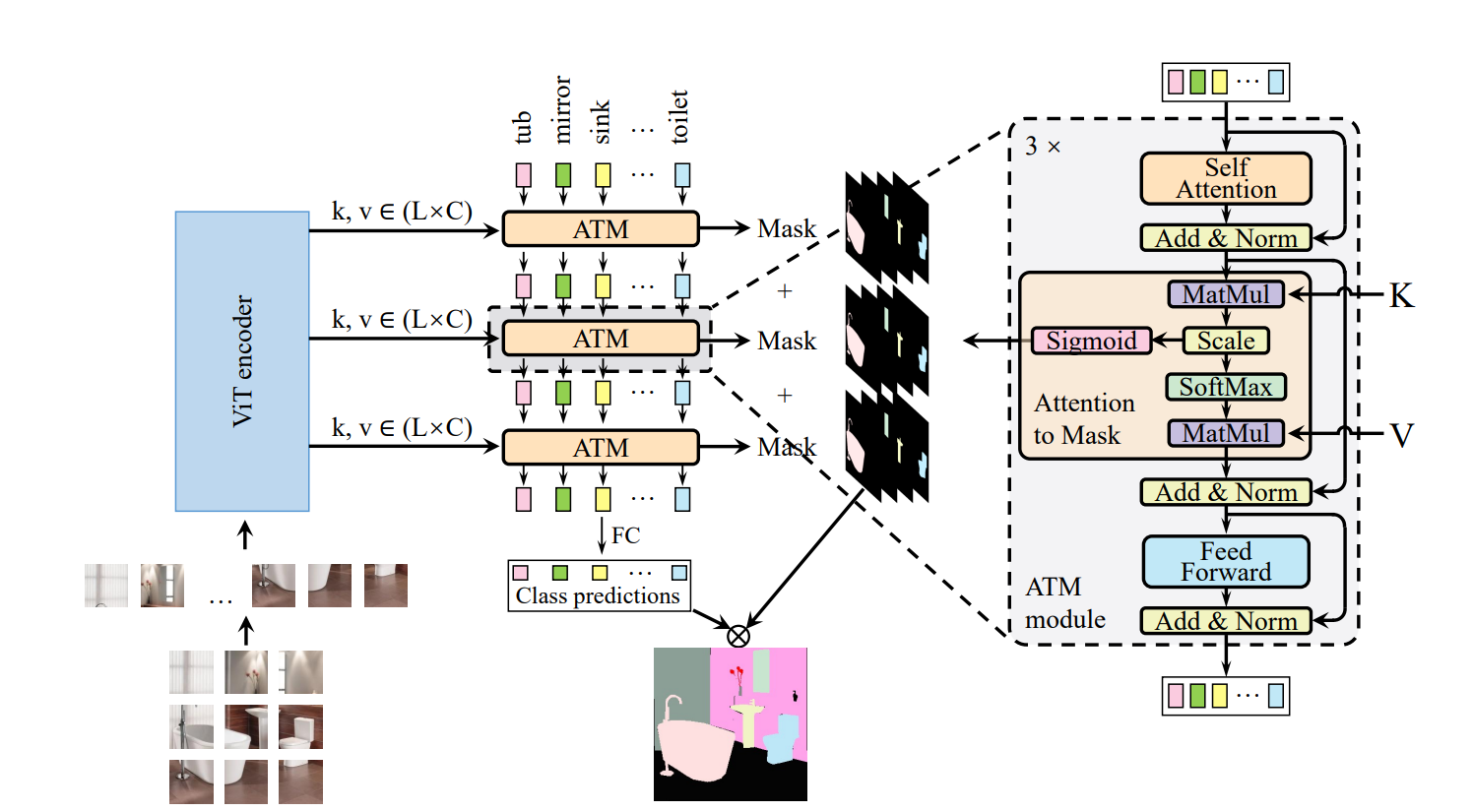

Mobile ViT

MobileViT block replaces local processing in convolutions with global processing using transformers.

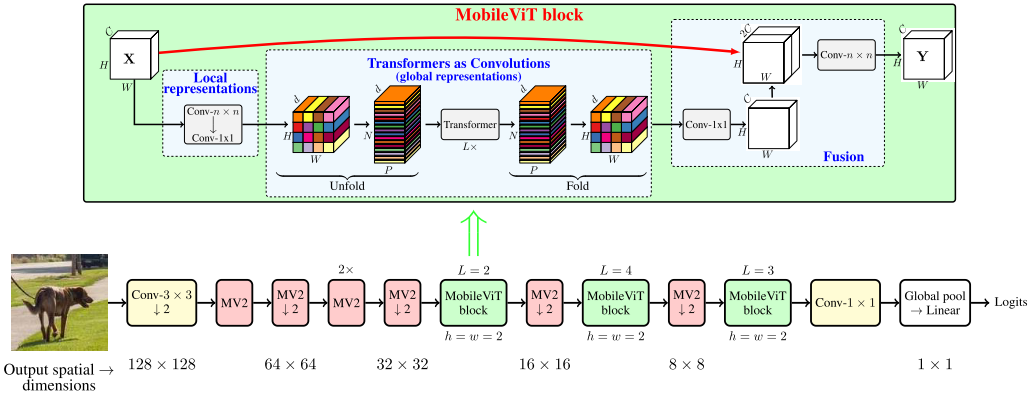
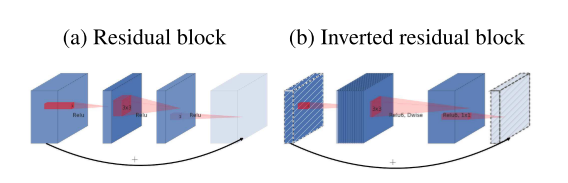
Bottleneck

Classical residuals connect the layers with a high number of channels, whereas inverted residuals connect the bottlenecks. This module takes as an input a low-dimensional compressed representation which is first expanded to a high dimension and filtered with a lightweight depthwise convolution.

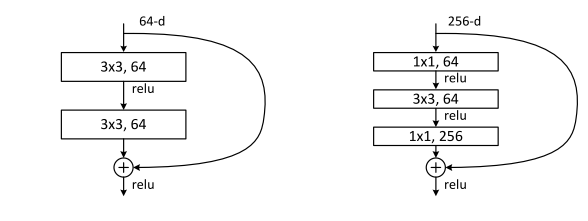
Kaiming He et al. used a bottleneck block, in which the middle operation contributes to smaller channels on the middle part.

spatial inductive biases (Conv weight has bias)

An inductive bias also known as learning bias, of a learning algorithm is the set of assumptions the leaner uses to predict outputs or given inputs that it has not encountered.

Local representation

Given $H \times W \times C$ tensor, MobileViT applies a $n\times n$ standard convolution layer followed by a point-wise (or $1 \times 1$) convolution layer to produce $H \times W \times d$ tensor. The first operation is used to encode local spatial information, and the second one is used to project the tensor to a high-dimension space ($d$ dimension, $d>C$).

Global representaion

The global info is encoded by learning inter-patch info by using transformers.
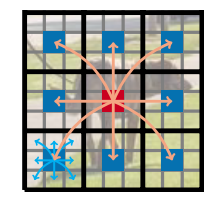
Local: among pixels (a small area of image)
Global: among patches (a whole area of image)

Global + local:
The red pixel can aggregate information from all pixels using local (cyan-colored arrows) and global (orange-colored arrows) information.

Reference

[1] Is the extra class embedding important to predict the results, why not simply use feature maps to predict?

[2] Whats the point of the class token here?

[3] Multilayer perceptron

[4] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, Ł. and Polosukhin, I., 2017. Attention is all you need. In Advances in neural information processing systems (pp. 5998-6008).

[5] Wiki: Inductive bias

[6] Howard, A., Sandler, M., Chu, G., Chen, L.C., Chen, B., Tan, M., Wang, W., Zhu, Y., Pang, R., Vasudevan, V. and Le, Q.V., 2019. Searching for mobilenetv3. In Proceedings of the IEEE/CVF international conference on computer vision (pp. 1314-1324).

[7] Mehta, S. and Rastegari, M., MobileViT: Light-weight, General-purpose, and Mobile-friendly Vision Transformer. In International Conference on Learning Representations.

[8] Zhang, B., Tian, Z., Tang, Q., Chu, X., Wei, X. and Shen, C., 2022. Segvit: Semantic segmentation with plain vision transformers. Advances in Neural Information Processing Systems, 35, pp.4971-4982.

[9] Train ViT on small datasets

[10] Goyal, A. and Bengio, Y., 2022. Inductive biases for deep learning of higher-level cognition. Proceedings of the Royal Society A, 478(2266), p.20210068.

[11] https://www.reddit.com/r/MLQuestions/comments/egof3l/explanation_of_inductive_bias/