There are some important mathematics about machine learning.

Regression

Linear regression

$$h_{\theta} (x) = \theta_0 + \theta_1 x$$

Non-linear regression

$$h_{\theta} (x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3$$

Logistic regression

Simultaneously update all $\theta_j$

$$\theta_j: = \theta_j - \alpha\sum^m_{i=1} (h_\theta (x^{(i)})-y^{(i)})x^{(i)}_j$$

Optimization logistic regression

$$\theta_j: = \theta_j - \alpha\frac{\partial}{\partial \theta_i} J(\theta)$$

Advantages:

no need to manually pick up $\alpha$

often faster than gradient descent

Disadvantages:

more complex

Cost function

Minimize cost function can minimize the error between predicted value and the real one.

Square error function

$$J(\theta_0, \theta_1) = \frac{1}{2m}\sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^2$$

If $\theta_0 = 0$,

$$J(\theta_1) = \frac{1}{2m}\sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^2$$

A loss function is a part of a cost function which is a type of an objective function.

See Objective function, cost function, loss function: are they the same thing?

Cost function for machine learning with regularization item:

$$J(\theta_1) = \frac{1}{m} [\sum^m_{i=1}\sum^K _ {k=1}(y^{(i)} _ k log(h _ {\theta}(x^{(i)})) _ k + (1 - y^{(i)})(1-h _ {\theta}(x^{(i)}) _ k)]$$

$$+ \frac{\lambda}{2m} \sum^{L-1} _ {l=1} \sum^{s _ l} _ {i=1} \sum^{s _ l + 1} _ {j=1} (\theta^{(l)} _ {ij})^2$$

Still do not regularize the bias term.

Gradient decent

$$\theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1) for j = 0, 1$$

linear regression

$$\frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1) = \frac{\partial}{\partial \theta_j}\frac{1}{2m}\sum^m_{i=1}(\theta_0 + \theta_1 x^{(i)} - y^{(i)})^2$$

• Need to choose $\alpha$.
• Needs many iterations.
• Works well even when is large $10^6$.

Logistic regression

$$h_{\theta} (x) = \frac{1}{1+e^{\theta^T x}}$$

Simplified (two classes, which is y = 0 or 1 always):

$$J(\theta) = \frac{1}{m}\sum^m_{i=1} Cost(h_{\theta} (x^{(i)}),(y^{(i)}))$$

Original version:

$$Cost(h_{\theta} (x) , y) = -y log(h_{\theta} (x) ) - (1-y)log(1-h_{\theta} (x) )$$

Call y,

$$Cost(h_{\theta} (x) , y) = \begin{cases}
-log(h_{\theta} (x)), & \text{if y = 0} \
-log(1 - h_{\theta} (x)), & \text{if y = 1}
\end{cases}$$

Normal equation

$$\theta = (X^TX)^{-1}X^T y$$

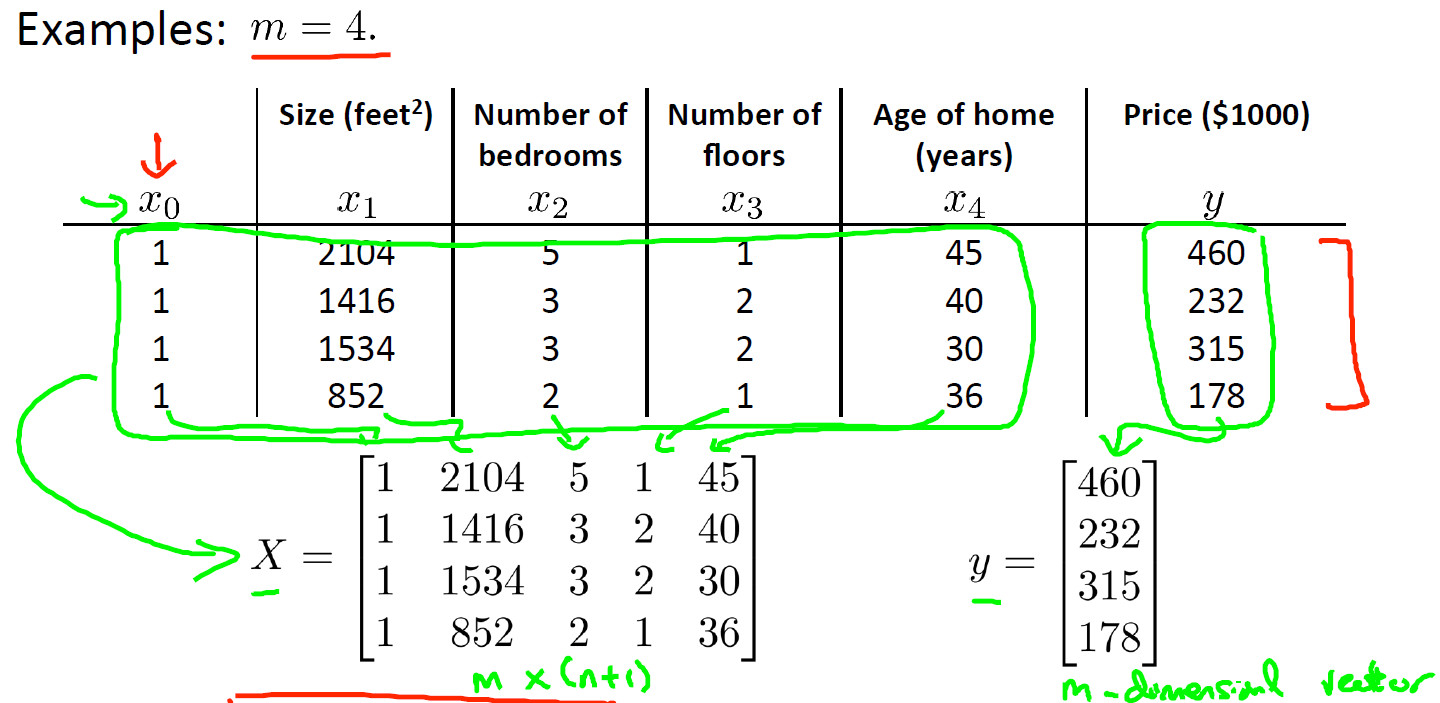
• No need to choose $\alpha$.
• Don’t needs to interate.

• Need to compute $(X^TX)^{-1}$

• Slow when is large.

Mean normalization

Replace $x_i$ with

$$\frac{x_i - \mu_i}{max - min}$$

Reference

[1] Andrew NG, [Machine learning](